Olá. Hoje vamos revisar como estimar um modelo de regressão linear por MQO no Python. Para isso, vamos usar pandas, scipy e a biblioteca statsmodels. Há algumas outras bibliotecas para estimação de modelos estatísticos em Python mas considero statsmodels a melhor delas pela facilidade e praticidade de uso. Outras bibliotecas como scikit-learn exigem um pouco mais de linhas de programação e, consequentemente, uma base matemática mais consolidada. Aliás, este é um ótimo exercício para quem está estudando modelos lineares: tente programá-lo no Python sem a ajuda dos comandos do pacote, from scratch. Sua compreensão vai melhorar bastante.
Antes de avançarmos para o código, vamos fazer uma breve revisão sobre os modelos lineares por MQO.
Regressão Linear por mínimos quadrados ordinários (MQO)
A regressão linear é um método de análise estatística que nos permite estimar o valor de uma determinada variável resposta (variável dependente) como função de outras variáveis preditoras (variáveis independentes). Essa relação pode ser expressa na seguinte equação:
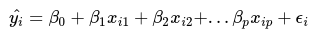
onde yi representa a variável dependente, xi1, xi2, xip representam as variáveis independentes, os preditores da regressão, b0 representa o intercepto da regressão, ou seja, o valor esperado de y quando todos os preditores tem valor = 0, b1, b2, bp representam os coeficientes estimados da regressão e epsilon representa o termo do erro, ou seja, a diferença entre os valores esperados e os valores observados de yi.
O método de estimação dos mínimos quadrados ordinários - MQO (do inglês ordinary least squares - OLS) é uma técnica de otimização que busca o melhor ajuste do modelo através da minimização dos quadrados do erro da regressão. A regressão linear é um método de análise bastante poderoso. Contudo, ela está ancorada em alguns pressupostos que precisam ser respeitados. Caso contrário, seus resultados tendem a ficar enviesados. São eles:
-
A relação entre a variável resposta e os preditores é linear.
-
A variável resposta possui distribuição normal. Os testes estatísticos desse método são todos baseados no pressuposto da normalidade. Caso tentemos analisar uma variável que não possui distribuição normal com esse método, os resultados não serão bons.
-
O termo do erro é não correlacionado com a variável resposta.
-
O termo do erro possui distribuição normal com média 0.
-
O termo do erro é homoscedástico, ou seja, possui variância constante em toda a sua extensão.
-
Os parâmetros populacionais são constantes, ou seja, valores fixos desconhecidos os quais serão estimados pela equação de regressão.
Estimando MQO no Python
Vamos aos códigos. Primeiro, vamos gerar algumas variáveis aleatórias distribuídas normalmente, uma variável categórica binária e um erro normalmente distribuído para servir de banco de dados para nossa regressão.
%matplotlib inline
import scipy as sp
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.formula.api as sm
x1 = sp.random.normal(size=100)
x2 = sp.random.normal(size=100)
x3 = sp.random.normal(size=100)
x4 = sp.random.normal(size=100)
categoria = sp.random.binomial(n=1, p=.5, size=100)
erro = sp.random.normal(size=100)
Em seguida, vamos construir a variável resposta com parâmetros conhecidos para fins de comparação. A equação verdadeira pode ser expressa assim:
y = 3 + 2(x1) + 0.65(x2) + 3.14(x3) - 1.75(x4) + 1.5(dummy) + epsilon
Vamos verificar, no final deste tutorial, o desempenho da análise de regressão em relação aos parâmetros verdadeiros.
y = 3 + 2*x1 + 0.65*x2 + 3.14*x3 - 1.75*x4 + 1.5*categoria + erro
Em seguida, vamos criar um DataFrame com essas variáveis.
dic = {"y":y, "x1":x1, "x2":x2, "x3":x3, "x4":x4, "categoria":categoria}
dados = pd.DataFrame(data=dic)
dados #Visualiza o DataFrame
| categoria | x1 | x2 | x3 | x4 | y | |
|---|---|---|---|---|---|---|
| 0 | 0 | -1.027964 | 0.005811 | 0.735222 | 0.613691 | 2.028470 |
| 1 | 1 | 1.193090 | 0.258837 | -0.017317 | -0.821739 | 8.377292 |
| 2 | 1 | 1.225674 | -2.640500 | -0.889131 | -2.218702 | 5.831579 |
| 3 | 1 | 1.288136 | 0.915106 | 1.903477 | 0.568446 | 13.142979 |
| 4 | 0 | -0.828994 | 0.148843 | 0.344978 | 0.051499 | 1.756007 |
| 5 | 0 | -0.007645 | -1.902100 | 0.942490 | -0.322518 | 5.588279 |
| 6 | 1 | 0.088384 | -2.736063 | -0.215483 | -0.588779 | 3.413264 |
| 7 | 0 | -0.847198 | -1.718300 | -1.105616 | -0.505273 | -1.082864 |
| 8 | 0 | -0.320159 | 1.756683 | 1.476829 | -1.037843 | 8.531030 |
| 9 | 1 | -0.487969 | -1.084512 | 1.147471 | 0.394563 | 5.768816 |
| 10 | 0 | -0.097839 | -0.655643 | -0.064105 | -1.649199 | 5.679842 |
| 11 | 0 | 0.955571 | -0.853956 | 0.749347 | -0.794555 | 6.654270 |
| 12 | 1 | -0.747153 | 0.861207 | 0.637005 | 0.879909 | 2.074678 |
| 13 | 1 | 1.184340 | -0.820462 | -0.798241 | 0.272143 | 2.424067 |
| 14 | 0 | -0.941562 | -0.717335 | -1.962072 | -2.679478 | -2.208384 |
| 15 | 0 | 0.061954 | 1.247335 | -2.059399 | 2.176928 | -7.798604 |
| 16 | 0 | 1.671110 | 1.880848 | -0.749895 | -0.011972 | 5.476915 |
| 17 | 0 | -0.720185 | -0.048464 | -3.682315 | 0.250626 | -9.847082 |
| 18 | 1 | -1.209025 | 0.594774 | 0.452681 | -0.639228 | 6.160792 |
| 19 | 0 | 0.666450 | 1.340304 | 1.219634 | 0.508693 | 7.987290 |
| 20 | 1 | -0.316183 | 0.288424 | 1.202293 | -1.018137 | 10.800371 |
| 21 | 1 | 0.172340 | -0.960865 | 0.552074 | -0.132070 | 7.261349 |
| 22 | 0 | 0.447723 | 0.817908 | -0.390960 | -0.497449 | 3.733669 |
| 23 | 1 | 0.369514 | 1.160988 | -0.036910 | -1.412312 | 10.157134 |
| 24 | 1 | 0.978639 | 1.002424 | -0.726037 | -0.222755 | 3.963156 |
| 25 | 0 | -1.301225 | 0.381227 | 1.235124 | 2.317437 | 0.102828 |
| 26 | 0 | -0.460727 | 0.415375 | -1.344034 | 0.129310 | -2.840350 |
| 27 | 0 | -1.674894 | -0.219167 | -1.130843 | -1.038059 | -3.399894 |
| 28 | 0 | 0.601086 | -0.880368 | -0.937390 | 0.869635 | 0.578146 |
| 29 | 1 | 0.519467 | 0.449896 | 0.026430 | 1.029819 | 6.766147 |
| ... | ... | ... | ... | ... | ... | ... |
| 70 | 0 | 0.120537 | -3.120954 | 1.473131 | 0.032333 | 6.469714 |
| 71 | 1 | 0.228711 | -0.008374 | 1.309662 | -0.660893 | 11.122802 |
| 72 | 1 | -1.976085 | 1.199087 | -0.390166 | 0.566129 | -1.789751 |
| 73 | 0 | 0.211299 | 1.664436 | -0.631966 | -0.107809 | 3.539535 |
| 74 | 0 | 0.672581 | 2.205682 | 0.844343 | 1.581004 | 7.127058 |
| 75 | 1 | -1.755712 | -0.159558 | -0.861777 | 0.688980 | -1.826065 |
| 76 | 0 | 0.576626 | 0.127073 | 0.850716 | 0.334624 | 6.482678 |
| 77 | 1 | -0.173947 | -0.407799 | 1.277835 | -0.174108 | 7.722501 |
| 78 | 1 | 1.793446 | 0.316700 | 1.076530 | 1.611143 | 9.772018 |
| 79 | 1 | -0.558026 | -0.178458 | -0.761499 | -0.015727 | -0.297279 |
| 80 | 0 | -0.682473 | 0.270851 | -0.954590 | -0.484107 | 0.030462 |
| 81 | 0 | -0.129743 | 1.089140 | -0.638405 | 1.458407 | -1.674821 |
| 82 | 0 | 0.592878 | -0.235288 | 0.035668 | -0.887291 | 5.730212 |
| 83 | 1 | -0.845119 | -0.332484 | 1.361238 | 0.195806 | 8.018649 |
| 84 | 0 | -1.032762 | 0.357636 | 0.218133 | -1.539139 | 3.772423 |
| 85 | 0 | 0.313567 | 0.156096 | -0.538710 | -0.090811 | 1.210189 |
| 86 | 0 | -1.606484 | 1.537090 | 0.326825 | -0.833555 | 2.607500 |
| 87 | 1 | 0.060540 | 1.158225 | -1.465049 | 0.788696 | -2.903798 |
| 88 | 0 | -0.557101 | 1.614070 | -2.133689 | -0.114207 | -3.198860 |
| 89 | 0 | 0.364759 | -0.754128 | -0.106209 | -0.626787 | 4.098707 |
| 90 | 1 | 0.519074 | -0.854893 | 1.054564 | 0.429074 | 6.553203 |
| 91 | 1 | 0.098454 | 1.064374 | -0.140774 | 0.533403 | 5.680029 |
| 92 | 0 | 1.435576 | -0.942384 | -1.706739 | 0.765818 | -0.339778 |
| 93 | 1 | 0.544879 | -0.614113 | -0.028148 | -1.792886 | 8.194594 |
| 94 | 0 | -0.835324 | 0.114021 | 0.304025 | 1.674463 | -1.785285 |
| 95 | 1 | -0.981402 | 0.348162 | -0.006721 | 0.343610 | 1.657995 |
| 96 | 1 | -0.275160 | 0.261869 | -2.552706 | -0.284243 | -3.720913 |
| 97 | 1 | 0.104991 | 0.547673 | 0.886136 | -1.270264 | 10.635857 |
| 98 | 1 | 0.006807 | -0.489711 | 0.319738 | 1.301208 | 0.025958 |
| 99 | 1 | -0.114278 | -0.511798 | 0.248029 | 0.973711 | 3.129828 |
100 rows × 6 columns
Prontinho. Agora, vamos dar uma olhada nas estatísticas descritivas e na distribuição da variável resposta. Lembre-se de que ela deve possuir distribuição normal.
print("Estatísticas descritivas de y:")
dados['y'].describe()
Estatísticas descritivas de y:
count 100.000000
mean 3.709140
std 4.417438
min -9.847082
25% 0.665959
50% 3.753046
75% 6.709719
max 13.142979
Name: y, dtype: float64
# Elabora um histograma
plt.hist(y, color='red', bins=15)
plt.title('Histograma da variável resposta')
plt.show()
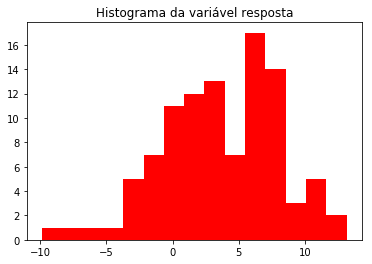
A distribuição da variável parece “bem normal”. Agora vamos estimar o modelo e mostrar os resultados.
reg = sm.ols(formula='y~x1+x2+x3+x4+categoria', data=dados).fit()
print(reg.summary())
| Dep. Variable: | y | R-squared: | 0.959 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.957 |
| Method: | Least Squares | F-statistic: | 442.1 |
| Date: | Sun, 25 Feb 2018 | Prob (F-statistic): | 1.17e-63 |
| Time: | 12:48:30 | Log-Likelihood: | -132.89 |
| No. Observations: | 100 | AIC: | 277.8 |
| Df Residuals: | 94 | BIC: | 293.4 |
| Df Model: | 5 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 2.6426 | 0.154 | 17.184 | 0.000 | 2.337 | 2.948 |
| x1 | 2.0440 | 0.100 | 20.403 | 0.000 | 1.845 | 2.243 |
| x2 | 0.7448 | 0.102 | 7.272 | 0.000 | 0.541 | 0.948 |
| x3 | 3.0630 | 0.094 | 32.739 | 0.000 | 2.877 | 3.249 |
| x4 | -1.8298 | 0.102 | -17.876 | 0.000 | -2.033 | -1.627 |
| categoria | 1.7417 | 0.193 | 9.014 | 0.000 | 1.358 | 2.125 |
| Omnibus: | 0.782 | Durbin-Watson: | 1.901 |
|---|---|---|---|
| Prob(Omnibus): | 0.676 | Jarque-Bera (JB): | 0.862 |
| Skew: | -0.100 | Prob(JB): | 0.650 |
| Kurtosis: | 2.591 | Cond. No. | 3.31 |
Vamos começar pela primeira tabela apresentada. As medidas mais importantes para nós neste momento são o R2 ajustado, a estatística de teste F, o p-valor dessa estatística e, caso queiramos comparar diferentes modelos, o log-likelihood, o Akaike Information Criterion (AIC) e o Bayesian Information Criterion (BIC).
O R2 ajustado nos dá uma medida de porcentagem da variância explicada pelo modelo. Este modelo tem um poder explicativo de 95,7%. Nada mau, hum? Mas não se engane! O R2 não é uma medida de ajuste mas apenas nos diz o quanto de nossos dados esse modelo explica. O restante do que falta explicar é atribuído ao termo do erro, ou seja, todas as outras coisas que tem influência sobre nossa variável resposta mas que não estão no modelo ou não podem de alguma forma ser mensuradas. Em ciências naturais é comum obtermos um R2 próximo de 100%. Já nas ciências sociais, costumamos ficar muito felizes quando conseguimos 30% da variância dos dados explicados. A natureza dos dados estudados é bem diferente. A estatística de teste F e seu p-valor < 0.001 basicamente nos mostram que esse modelo é estatisticamente válido.
Quanto aos coeficientes da regressão, os betas estimados, vejam os resultados. Parecem bem confiáveis, não é mesmo? O modelo pegou muito bem as rlações entre as variáveis e os valores verdadeiros estão todos dentro do intervalo de confiança estimado. Podemos interpretá-los da seguinte forma: quando todos os preditores são iguais a 0, o valor esperado de y é 2,64. Para cada aumento de 1 unidade em x1, y aumenta, em média, 2,04. Para cada aumento de 1 unidade em x2, y aumenta, em média, 0,74. Para cada aumento de 1 unidade em x3, y aumenta, em média, 3,06. Para cada aumento de 1 unidade em x4, y diminui (veja o sinal negativo no coeficiente), em média, 1,83. A variável categórica possui uma análise diferente. Os casos da categoria 1 y têm um valor esperado médio 1,74 maior do que os casos da categoria 0. O p-valor para todas os coeficientes estimados é menor que 0.001 o que mostra que eles são estatisticamente significativos.
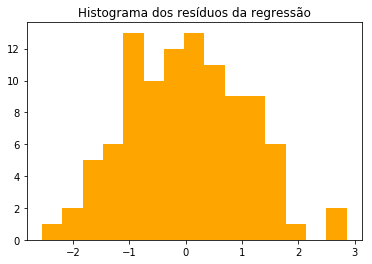
Vamos agora plotar alguns gráficos de avaliação. Primeiro, vamos plotar um histograma dos resíduos (epsilon = y - ŷ). Lembre-se de que os resíduos precisam ter distribuição normal com média 0. Em seguida, vamos plotar um gráfico de dispersão (scatterplot) dos dos valores preditos (ŷ) e resíduos. É preciso que os resíduos e a variável resposta sejam não correlacionados.
y_hat = reg.predict()
res = y - y_hat
plt.hist(res, color='orange', bins=15)
plt.title('Histograma dos resíduos da regressão')
plt.show()
plt.scatter(y=res, x=y_hat, color='green', s=50, alpha=.6)
plt.hlines(y=0, xmin=-10, xmax=15, color='orange')
plt.ylabel('$\epsilon = y - \hat{y}$ - Resíduos')
plt.xlabel('$\hat{y}$ ou $E(y)$ - Predito')
plt.show()
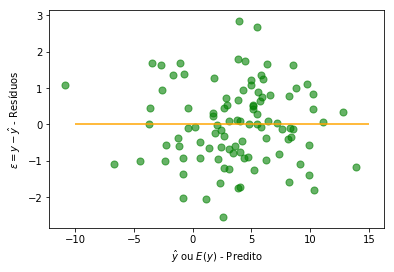
Agora, vamos observar apresentar apenas os coeficientes da regressão se quisermos facilitar a análise e traçar a reta de regressão entre as variáveis y e x1.
coefs = pd.DataFrame(reg.params)
coefs.columns = ['Coeficientes']
print(coefs)
Coeficientes
Intercept 2.964863
x1 2.083678
x2 0.751478
x3 3.229035
x4 -1.880821
categoria 1.378816
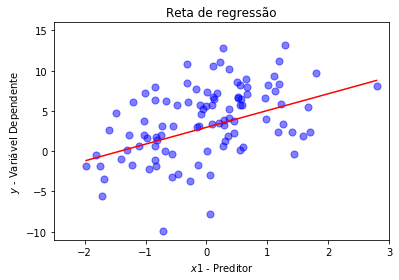
plt.scatter(y=dados['y'], x=dados['x1'], color='blue', s=50, alpha=.5)
X_plot = sp.linspace(min(dados['x1']), max(dados['x1']), len(dados['x1']))
plt.plot(X_plot, X_plot*reg.params[1] + reg.params[0], color='r')
plt.ylim(-11,16)
plt.xlim(-2.5,3)
plt.title('Reta de regressão')
plt.ylabel('$y$ - Variável Dependente')
plt.xlabel('$x1$ - Preditor')
plt.show()