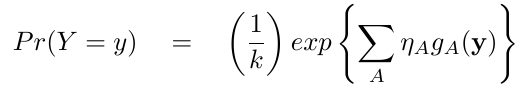Neste post abordaremos a última palavra em modelos estatísticos para dados relacionais os exponential random graph models, ou modelos p* (pê-estrela). Iniciaremos com um post mais técnico focado nos comandos e possíveis parâmetros do pacote statnet. No próximo post, abordaremos questões mais conceituais relacionadas aos modelos bem como sua interpretação.
Para ver uma versão deste post organizado num belo e eficiente layout chamado Tufte Handout inspirado nos livros e comunicações do prof. Edward Tufte, acesse aqui.
Os modelos p* foram desenvolvidos para dar conta de dados que assumem interdependência das observações. Ora, os modelos econométricos clássicos (regressão linear, regressão logística, etc.) assumem independência das observações e portanto não devem ser aplicados a dados relacionais. Em outras palavras, se A conhece C, a existência de um laço entre B e C altera a probabilidade de existência de um laço entre B e A[1].
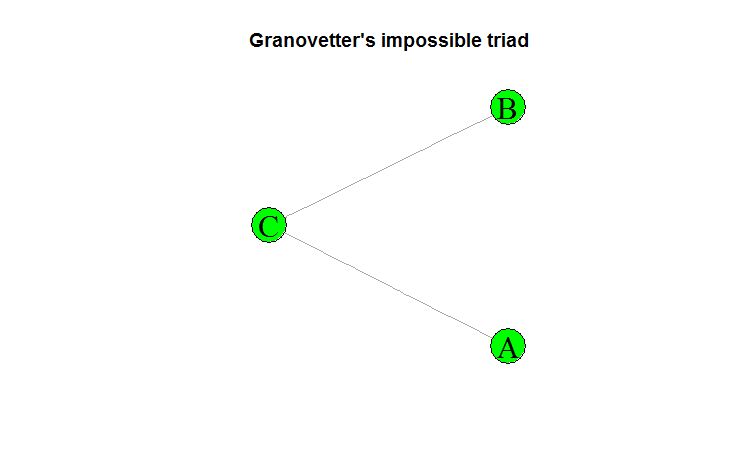
O modelo p* pode ser definido por
onde Y é o grafo teórico simulado, y é o grafo observado, ΣA é a soma de todas as configurações A, ηA é o parâmetro estimado correpondente à configuração A, gA(y) é a estatística da configuração A observada no grafo y e k é uma constante que assegura a distribuição de probabilidades[2].
Para estimar um modelo p* no R, usaremos os comandos da suite statnet e o pacote igraph para auxílio com a importação dos dados quando for o caso. Vamos ao primeiro exemplo.
ERGM - Florentine Families
Vamos tentar modelar a rede casamentos de famílias de Florença do famoso trabalho de Padgett (1994)[3]. Primeiro, investiguemos a rede.
library(statnet)
library(sand)
library(intergraph)
data(florentine)
flomarriage
## Network attributes:
## vertices = 16
## directed = FALSE
## hyper = FALSE
## loops = FALSE
## multiple = FALSE
## bipartite = FALSE
## total edges= 20
## missing edges= 0
## non-missing edges= 20
##
## Vertex attribute names:
## priorates totalties vertex.names wealth
##
## No edge attributes
plot(flomarriage, displaylabels=T,
label.cex=0.8, main="Padgett Florentine Families")
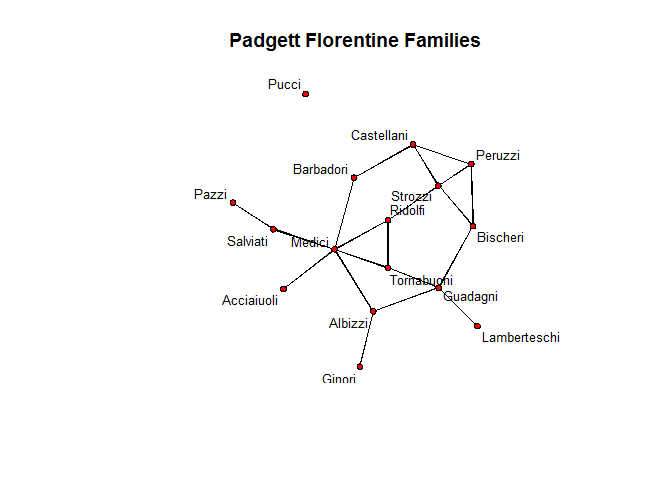
Investiguemos agora os atributos. Como acho mais fácil fazer isso usando o pacote igraph, vamos a ele.
marriage <- asIgraph(flomarriage)
V(marriage)$priorates
## [1] 53 65 0 12 22 0 21 0 53 0 42 0 38 35 74 0
V(marriage)$totalties
## [1] 2 3 14 9 18 9 14 14 54 7 32 1 4 5 29 7
V(marriage)$wealth
## [1] 10 36 55 44 20 32 8 42 103 48 49 3 27 10 146 48
Podemos plotar a rede representando algum atributo. Vamos representar a riqueza com o tamanho dos vértices. Como o pacote igraph lê os valores absolutos e o grafo fica muito poluído, vamos dividir o vetor de valores de riqueza por 4 para uma visualização mais limpa.
plot(marriage, vertex.label.cex=0.9,
vertex.label=V(marriage)$vertex.names,
vertex.size=V(marriage)$wealth/4,
vertex.color="lightblue",
vertex.label.color="black",
main = "Padgett Florentine Families",
xlab="Size = Wealth")
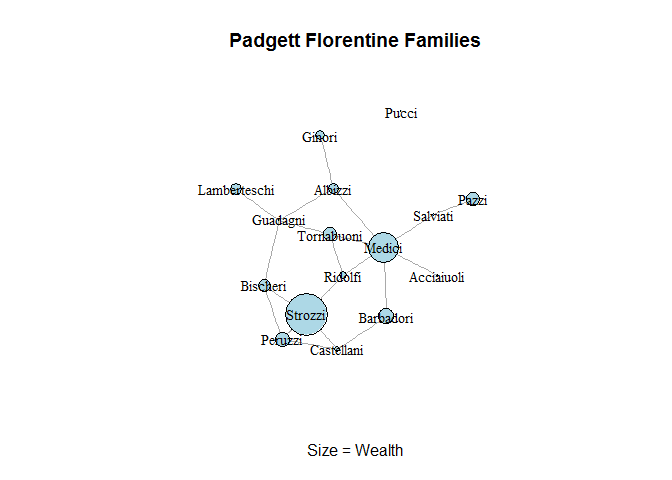
Agora vamos à modelagem. Primeiro, é comum estimarmos o modelo nulo[4], ou seja, um modelo apenas com o parâmetro edges que corresponde ao intercepto dos modelos econométricos comuns. Este modelo toma a díade por unidade de análise e estima a “propensão dos atores a escolherem outros atores, serem escolhidos por outros, a fazer escolhas recíprocas e a tendência média (parâmetro de densidade) a interagir com os outros (Lazega & Higgins, 2014, p. 81)[5].
fit1 <- ergm(flomarriage~edges)
summary(fit1)
##
## ==========================
## Summary of model fit
## ==========================
##
## Formula: flomarriage ~ edges
##
## Iterations: 5 out of 20
##
## Monte Carlo MLE Results:
## Estimate Std. Error MCMC % p-value
## edges -1.6094 0.2449 0 <1e-04 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Null Deviance: 166.4 on 120 degrees of freedom
## Residual Deviance: 108.1 on 119 degrees of freedom
##
## AIC: 110.1 BIC: 112.9 (Smaller is better.)
O parâmetro negativo e significativo nos mostra que esta rede se desenvolve com menos laços entre seus atores do que esperaríamos numa rede aleatória[6]. Em seguida, vamos estimar um modelo controlando por triângulos e por distribuição de laços compartilhados geometricamente pesada[7] (gwesp). Vamos usar os comandos formula e summary.statistics para contar as estatísticas existentes na rede original.
model2 <- formula(flomarriage~edges+triangle+
gwesp(1,fixed=T))
summary.statistics(model2)
## edges triangle gwesp.fixed.1
## 20.000000 3.000000 8.632121
Em seguida, “rodamos” o modelo.
fit2 <- ergm(model2)
summary(fit2)
##
## ==========================
## Summary of model fit
## ==========================
##
## Formula: flomarriage ~ edges + triangle + gwesp(1, fixed = T)
##
## Iterations: 2 out of 20
##
## Monte Carlo MLE Results:
## Estimate Std. Error MCMC % p-value
## edges -1.7424 0.3733 0 <1e-04 ***
## triangle -4.6371 7.8862 0 0.558
## gwesp.fixed.1 1.8157 2.8884 0 0.531
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Null Deviance: 166.4 on 120 degrees of freedom
## Residual Deviance: 107.6 on 117 degrees of freedom
##
## AIC: 113.6 BIC: 122 (Smaller is better.)
Às vezes é útil avaliar o processo de amostragem por Monte Carlo Markov Chain (MCMC). Para isso, usamos o comando plot().
plot(fit2)
## Sample statistics summary:
##
## Iterations = 16384:4209664
## Thinning interval = 1024
## Number of chains = 1
## Sample size per chain = 4096
##
## 1. Empirical mean and standard deviation for each variable,
## plus standard error of the mean:
##
## Mean SD Naive SE Time-series SE
## edges -0.02808 4.011 0.06266 0.06266
## triangle -0.03198 1.950 0.03047 0.03047
## gwesp.fixed.1 -0.12463 5.376 0.08400 0.08400
##
## 2. Quantiles for each variable:
##
## 2.5% 25% 50% 75% 97.5%
## edges -8.000 -3 0.000e+00 3 8.00
## triangle -3.000 -1 0.000e+00 1 4.00
## gwesp.fixed.1 -8.632 -3 2.409e-13 3 11.63
##
##
## Sample statistics cross-correlations:
## edges triangle gwesp.fixed.1
## edges 1.0000000 0.7350670 0.7410482
## triangle 0.7350670 1.0000000 0.9978614
## gwesp.fixed.1 0.7410482 0.9978614 1.0000000
##
## Sample statistics auto-correlation:
## Chain 1
## edges triangle gwesp.fixed.1
## Lag 0 1.000000000 1.000000000 1.000000000
## Lag 1024 0.009105098 0.006407971 0.006171425
## Lag 2048 -0.025615341 -0.023582057 -0.023856444
## Lag 3072 0.012069051 0.023109858 0.022171381
## Lag 4096 0.001542952 -0.009649964 -0.010962329
## Lag 5120 -0.004242831 -0.009134193 -0.008909237
##
## Sample statistics burn-in diagnostic (Geweke):
## Chain 1
##
## Fraction in 1st window = 0.1
## Fraction in 2nd window = 0.5
##
## edges triangle gwesp.fixed.1
## 1.0923 0.1873 0.1368
##
## Individual P-values (lower = worse):
## edges triangle gwesp.fixed.1
## 0.2747163 0.8514111 0.8911700
## Joint P-value (lower = worse): 0.3727567 .
## Loading required namespace: latticeExtra
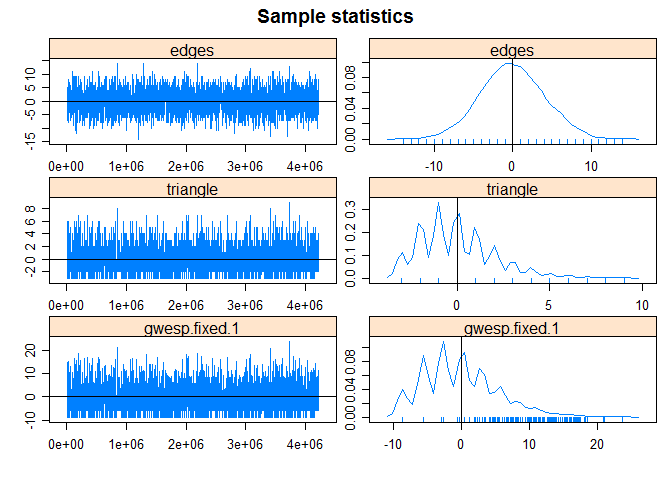
Para verificar o ajuste e a convergência do modelo, usamos o comando gof().
gof2 <- gof(fit2)
par(mfrow=c(1,3))
plot(gof2)
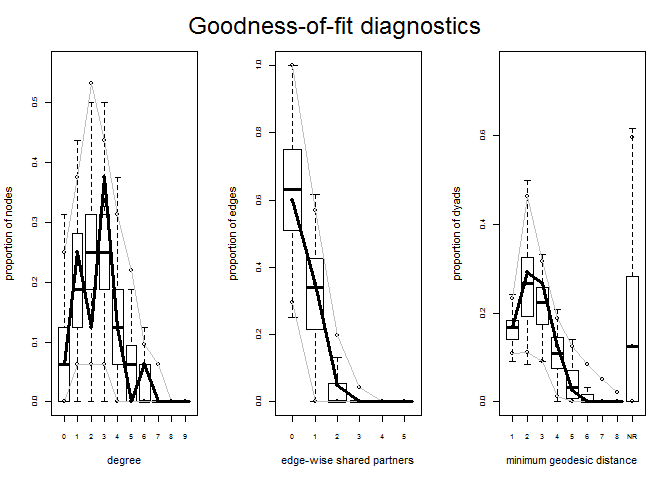
O modelo parece se ajustar bem aos dados. Este modelo convergiu e podemos confiar nos parâmetros estimados para explicar a emergência de nossa rede observada. Neste caso, observando os resultados, apesar de triângulos e distribuição de laços compartilhados terem estimadores respectivamente negativo e postivo, eles não são estatisticamente significativos indicando que essas configurações não são importantes para entendermos o surgimento da rede.
Agora, como outro exemplo, vamos trabalhar com os dados dos advogados de Lazega.
ERGM - Lazega’s lawyers
Estes dados estão no pacote sand. Precisamos transformá-los num objeto de classe network para realizar a estimação do p*.
lazega <- upgrade_graph(lazega)
lawyers <- asNetwork(lazega)
fit1 <- ergm(lawyers~edges)
summary(fit1)
##
## ==========================
## Summary of model fit
## ==========================
##
## Formula: lawyers ~ edges
##
## Iterations: 5 out of 20
##
## Monte Carlo MLE Results:
## Estimate Std. Error MCMC % p-value
## edges -1.4992 0.1031 0 <1e-04 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Null Deviance: 873.4 on 630 degrees of freedom
## Residual Deviance: 598.8 on 629 degrees of freedom
##
## AIC: 600.8 BIC: 605.2 (Smaller is better.)
Depois de estimar o modelo P1, vamos estimar um modelo com triângulos e distribuição de laços compartilhados.
model2 <- formula(lawyers~edges+triangle+
gwesp(1,fixed=T))
summary.statistics(model2)
## edges triangle gwesp.fixed.1
## 115.0000 120.0000 213.1753
fit2 <- ergm(model2)
summary(fit2)
##
## ==========================
## Summary of model fit
## ==========================
##
## Formula: lawyers ~ edges + triangle + gwesp(1, fixed = T)
##
## Iterations: 2 out of 20
##
## Monte Carlo MLE Results:
## Estimate Std. Error MCMC % p-value
## edges -3.6696 0.3120 0 <1e-04 ***
## triangle -0.2200 0.2129 0 0.302
## gwesp.fixed.1 0.9804 0.2463 0 <1e-04 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Null Deviance: 873.4 on 630 degrees of freedom
## Residual Deviance: 519.8 on 627 degrees of freedom
##
## AIC: 525.8 BIC: 539.1 (Smaller is better.)
Vamos ver o ajuste desse modelo aos dados e sua convergência.
gof2 <- gof(fit2)
par(mfrow=c(1,3))
plot(gof2)
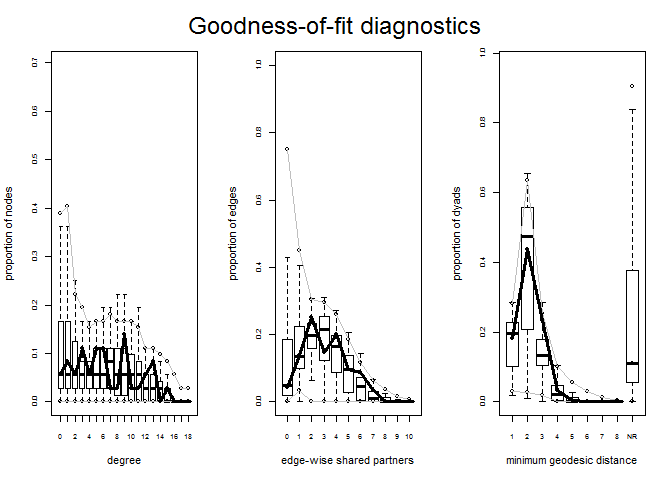
Vamos tentar elaborar um modelo um pouco mais complexo usando algumas estatísticas a mais além dos atributos dos atores. Dessa vez vamos modelar ainda a distribuição de grau e os atributos gênero, escritório que pertence, escola de origem, idade e senioridade. Atributos qualitativos são inseridos no modelo por semelhança. Atributos quantitativos são inseridos, neste caso, somando-se os valores de díades para todos os atores na rede. A lista de estatísticas possíveis é longa e podemos investigá-la com o comando help("ergm-terms"). Vamos ao modelo:
model3 <- formula(lawyers~edges+triangle+
gwesp(1,fixed=T)+gwdegree(1,fixed=T)+
nodematch("Gender")+nodematch("Office")+
nodematch("School")+nodecov("Age")+
nodecov("Seniority"))
summary.statistics(model3)
## edges triangle gwesp.fixed.1 gwdegree
## 115.0000 120.0000 213.1753 79.2000
## nodematch.Gender nodematch.Office nodematch.School nodecov.Age
## 99.0000 85.0000 36.0000 10526.0000
## nodecov.Seniority
## 4687.0000
fit3 <- ergm(model3)
summary(fit3)
##
## ==========================
## Summary of model fit
## ==========================
##
## Formula: lawyers ~ edges + triangle + gwesp(1, fixed = T) + gwdegree(1,
## fixed = T) + nodematch("Gender") + nodematch("Office") +
## nodematch("School") + nodecov("Age") + nodecov("Seniority")
##
## Iterations: 3 out of 20
##
## Monte Carlo MLE Results:
## Estimate Std. Error MCMC % p-value
## edges 1.348214 2.393001 0 0.573367
## triangle -0.142962 0.216670 0 0.509616
## gwesp.fixed.1 0.936593 0.275091 0 0.000705 ***
## gwdegree 0.462105 0.632732 0 0.465462
## nodematch.Gender 0.339332 0.214801 0 0.114673
## nodematch.Office 0.990756 0.179510 0 < 1e-04 ***
## nodematch.School -0.004922 0.253659 0 0.984524
## nodecov.Age -0.053593 0.018657 0 0.004211 **
## nodecov.Seniority -0.025914 0.015030 0 0.085180 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Null Deviance: 873.4 on 630 degrees of freedom
## Residual Deviance: 475.5 on 621 degrees of freedom
##
## AIC: 493.5 BIC: 533.6 (Smaller is better.)
Para exemplos de interpretação, veja Lusher, Koskinen & Robins (2012) e Salej Higgins et al (2014)[8]
Vamos agora investigar o ajuste do modelo aos dados e sua convergência.
gof3 <- gof(fit3)
par(mfrow=c(1,3))
plot(gof3)
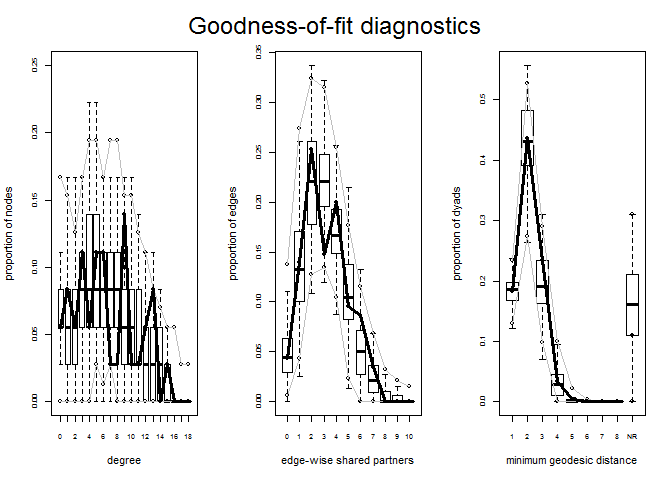
Quando trabalhamos com modelos p*, as possibilidades são enormes. Devemos testar várias configurações de estatísticas modeladas de acordo com o que pretendemos investigar na rede em questão e com o ajuste do modelo aos dados.
Algoritmos
O algoritmo default pelo qual o pacote statnet realiza a estimação dos modelos p* é o Geyer-Thompson (1992) (MCMLE)[9]. Este algoritmo costuma retornar os melhores resultados mas, por ser extremamente exigente (os modelos devem convergir 2 vezes, do contrário, o comando dá erro e para) pode não rodar para algumas redes mais extensas. O pacote statnet permite o uso de mais três algoritmos além do MCMLE: o algoritmo Robbins-Monro (usado pela família de softwares PNET), Metropolis-Hastings (aproximação estocástica) e Stepping. Vamos realizar a estimação do modelo 3 para os dados de Lazega com os outros 3 algoritmos e vamos compará-los.
fit3.rb <- ergm(model3,
control=control.ergm(main.method = "Robbins-Monro"))
fit3.sa <- ergm(model3,
control=control.ergm(main.method = "Stochastic-Approximation"))
fit3.step <- ergm(model3,
control=control.ergm(main.method = "Stepping"))
library(texreg)
htmlreg(list(fit3, fit3.rb, fit3.sa, fit3.step),
single.row=T, caption.above = T,
custom.model.names=c("Geyer-Thompson", "Robbins-Monro","Metropolis-Hastings","Stepping"))
| Geyer-Thompson | Robbins-Monro | Metropolis-Hastings | Stepping | ||
|---|---|---|---|---|---|
| edges | 1.35 (2.39) | 0.90 | -0.17 (2.61) | 0.88 (2.37) | |
| triangle | -0.14 (0.22) | 0.12 | -0.00 (0.22) | -0.10 (0.20) | |
| gwesp.fixed.1 | 0.94 (0.28)*** | 0.69 | 0.79 (0.31)* | 0.88 (0.25)*** | |
| gwdegree | 0.46 (0.63) | 0.90 | 1.16 (0.72) | 0.37 (0.60) | |
| nodematch.Gender | 0.34 (0.21) | 0.35 | 0.32 (0.23) | 0.34 (0.22) | |
| nodematch.Office | 0.99 (0.18)*** | 1.33 | 0.70 (0.21)** | 0.97 (0.19)*** | |
| nodematch.School | -0.00 (0.25) | -0.36 | 0.06 (0.23) | -0.02 (0.26) | |
| nodecov.Age | -0.05 (0.02)** | -0.05 | -0.04 (0.02)* | -0.05 (0.02)** | |
| nodecov.Seniority | -0.03 (0.02) | -0.01 | -0.02 (0.02) | -0.02 (0.02) | |
| AIC | 493.54 | 507.18 | 511.53 | 494.43 | |
| BIC | 533.55 | 547.19 | 551.54 | 534.44 | |
| Log Likelihood | -237.77 | -244.59 | -246.76 | -238.21 | |
| ***p < 0.001, **p < 0.01, *p < 0.05 | |||||
Vamos verificar o ajuste dos modelos estimados com os outros algoritmos.
gof3.rb <- gof(fit3.rb)
gof3.sa <- gof(fit3.sa)
gof3.step <- gof(fit3.step)
par(mfrow=c(1,3))
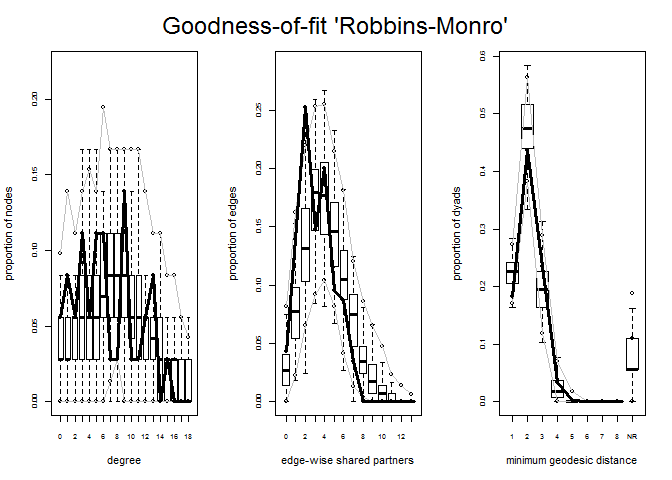
plot(gof3.rb,
main = "Goodness-of-fit 'Robbins-Monro'")
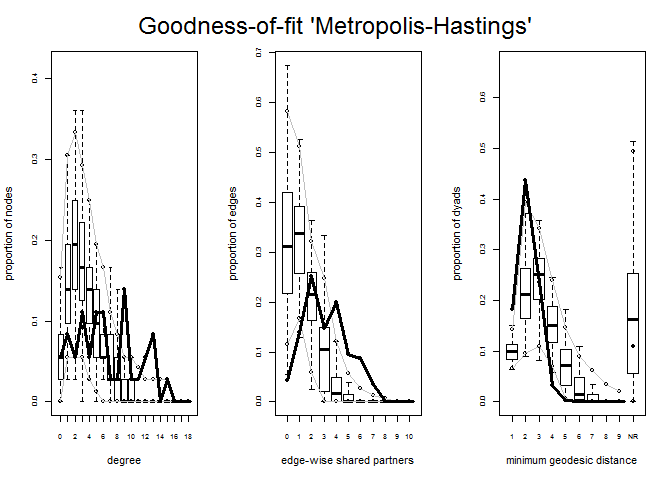
plot(gof3.sa,
main = "Goodness-of-fit 'Metropolis-Hastings'")
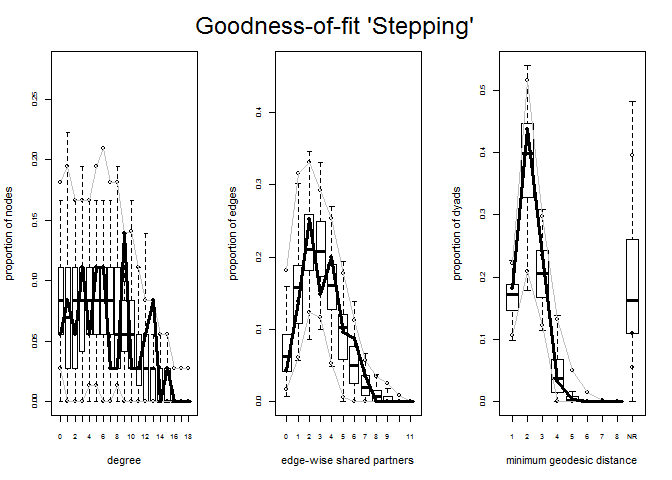
plot(gof3.step,
main="Goodness-of-fit 'Stepping'")
É importante lembrar que…
A estimação de um modelo p* pode ser um processo longo e cansativo. Não há testes ou métodos para escolha prévia de um modelo a não ser o bom e velho “tentativa e erro”. A partir do seu problema de pesquisa, escolha os parâmetros que deseja estimar e vá melhorando o modelo escolhendo outros parâmetros. Muita atenção: o modelo deve convergir e os parâmetros estimados devem estar dentro dos limites dos plots de Goodness-of-fit. O algoritmo Geyer-Thompson tem a vantagem (ou não) de não rodar quando o modelo não converge. Os outros algoritmos rodam de qualquer modo e checamos se o modelo está degenerado pelo GOF. É importantíssimo salientar que o modelo deve convergir completamente. Um modelo que não converge em algum de seus parâmetros não quer dizer absolutamente nada (Lusher, Koskinem & Robins, 2012)[10].
[1] Granovetter, M. S. (1973). The strength of weak ties. American journal of sociology, 1360-1380.
[2] Robins, Garry et al. An introduction to exponential random graph (p*) models for social networks. Social networks, Elsevier, v. 29, n. 2, p. 173–191, 2007.
[3] Padgett, John F. (1994) Marriage and Elite Structure in Renaissance Florence, 1282-1500. Paper delivered to the Social Science History Association.
[4] Este modelo é também conhecido como P1 e foi desenvolvido por Holland e Leinhardt.
[5] Lazega, E., & Higgins, S. S. (2014). Redes sociais e estruturas relacionais. Belo Horizonte, MG: Fino Traço.
[6] No próximo post pretendo explicar melhor o conceito teórico de rede aleatória e como ele é mobilizado na interpretação dos ERGMs.
[7] Geometrically weighted edgewise shared partner distribution.
[8] Salej Higgins, S., Ribeiro, A., Botrel de Vasconcellos, M., & Estevão Barbosa, J. (2014). L’émergence d’une structure cœur-périphérie dans un réseau brésilien de copublications en sciences comptables. Communiquer. Revue de communication sociale et publique, (12), 43-60.
[9] Lusher, D., Koskinen, J., & Robins, G. (2012). Exponential random graph models for social networks: Theory, methods, and applications. Cambridge University Press.
[10] Lusher, D., Koskinen, J., & Robins, G. (2012). Exponential random graph models for social networks: Theory, methods, and applications. Cambridge University Press.