Olá. Este é o primeiro de uma série de 5 posts onde abordarei algumas técnicas em Análise de Redes Sociais no R. Esse Workshop surgiu a partir de trabalhos de pesquisa do GIARS - Grupo Interdisciplinar de Pesquisa em Análise de Redes Sociais da UFMG, coordenado pelo prof. Silvio Salej Higgins. Como a maior parte da comunidade de analistas de redes usa prioritariamente dois softwares, a saber, Pajek e Ucinet, começarei abordando integrações entre esses programas e o R visando aqueles que já estão pensando em migrar.
Introdução
A linguagem R é uma linguagem de programação orientada a objetos bastante poderosa para modelagem estatística e elaboração de gráficos avançados. O R é um projeto GNU similar à linguagem S que foi desenvolvida nos Bell Laboratories por John Chambers e sua equipe (R CORE TEAM, 2016).
Por que usar o R?
Se já existem dois bons softwares para ARS e o PNET para estimar modelos p*, porque gostaríamos de trabalhar com R? Em primeiro lugar, o R é uma linguagem de código aberto. Apesar de não haver nenhuma garantia, a comunidade de usuários é gigantesca e qualquer dúvida postada nos fóruns de discussão dificilmente leva mais do que alguns minutos para obter uma resposta. Segundo, o R é uma ferramenta que integra todas as funcionalidades dos outros softwares, ou seja, ele gera visualizações, medidas descritivas, modelos estatísticos e (o que os outros não fazem) realiza mineração de dados. É possível desenvolver um projeto de pesquisa inteiro dentro do R sem ter que recorrer a outras ferramentas. Além disso, o R é compativel com qualquer sistema (Linux, Mac ou Windows). Infelizmente o Pajek e o Ucinet só funcionam em Windows.
Para trabalhar com dados em rede no R, usaremos basicamente dois pacotes: o pacote igraph e o pacote network. Concentraremos nossos esforços no início em entender bem o pacote igraph.
igraph
O pacote igraph é uma coleção de ferramentas para análise de dados relacionais buscando eficiência, portabilidade e facilidade. A biblioteca é compatível com as linguagens R, Python e C/C++ (CSARDI & NEPUSZ, 2006).
Entrada de Dados
Para começar, vamos experimentar algumas integrações com o Pajek. Integrações com o Ucinet serão abordadas no próximo post. No Pajek é bastante fácil exportar dados para o R. Na tela inicial do software, clique em tools depois em R, depois em send to R e escolha o que deseja enviar. Hoje vamos enviar apenas a rede ativa. Para esse exemplo, vou usar a minha rede pessoal mapeada em 2014 (já está bem desatualizada mas para os fins desse tutorial é suficiente).
Em seguida, copie o endereço que aparecerá na tela de resultados (log) e use-o para importar a rede no R com o comando source. Se você for um usuário do sistema Windows, não se esqueça de inverter as barras.
source("C:/Users/.../AppData/Local/Pajek/PajekR.r")
## ########################################
## R called from Pajek
## http://mrvar.fdv.uni-lj.si/pajek/
## Andrej Mrvar & Vladimir Batagelj
## University of Ljubljana, Slovenia
## -----------------------------------------------------------------------
## The following networks/matrices read:
## n1 : C:/Users/Neylson/Documents/UCINET Data/REDE_NEILSON_SEM_ISOLADOS_E_SEM_REPETIDO.net (83)
##
## Use objects() to get list of available objects
## Use comment(?) to get information about selected object
## Use savevector(v?,'???.vec') to save vector to Pajek input file
## Use savematrix(n?,'???.net') to save matrix to Pajek input file (.MAT)
## savematrix(n?,'???.net',2) to request a 2-mode matrix (.MAT)
## Use savenetwork(n?,'???.net') to save matrix to Pajek input file (.NET)
## savenetwork(n?,'???.net',2) to request a 2-mode network (.NET)
## Use v?<-loadvector('???.vec') to load vector(s) from Pajek input file
## Use n?<-loadmatrix('???.mat') to load matrix from Pajek input file
## -----------------------------------------------------------------------
Vemos que foi exportada uma matriz nomeada n1. Para darmos uma olhada na matriz, podemos usar o comando View. Usamos dim para ver as dimensões da matriz.
View(n1)
dim(n1)
## [1] 83 83
Para trabalhar com dados relacionais, precisamos transformar a matriz em um objeto de classe igraph. É necessário também especificar se trata-se de uma rede direcionada ou não. Primeiro carregamos o pacote no R. Se não tiver o pacote instalado, use o código install.packages(“igraph”).
library(igraph)
rede <- graph_from_adjacency_matrix(n1, mode="undirected", weighted = T)
Em seguida, podemos obter algumas informações sobre a rede importada apenas chamando o objeto rede criado.
rede
## IGRAPH UNW- 83 603 --
## + attr: name (v/c), weight (e/n)
## + edges (vertex names):
## [1] Isabela Crepalde--Isabela Crepalde
## [2] Isabela Crepalde--Sarah Crepalde
## [3] Isabela Crepalde--Tânia R. Costa
## [4] Isabela Crepalde--Sueli Crepalde
## [5] Isabela Crepalde--Gabriela Crepalde
## [6] Isabela Crepalde--João Pedro Batista
## [7] Sarah Crepalde --Guilherme Castro
## [8] Sarah Crepalde --Avelar Junior
## + ... omitted several edges
Identifiquei que há um loop que não desejamos. Vamos retirá-lo com o comando simplify.
rede <- simplify(rede)
Para importarmos do Ucinet, podemos apenas exportar a rede trabalhada para o Pajek e executar o mesmo procedimento descrito acima.
Caso estejamos interessados em trabalhar com modelos p*, é necessário que usemos o pacote network. para isso podemos usar um comando simples.
library(statnet)
net <- network(n1, directed = FALSE)
Visualizações
A visualização default do igraph pode ser obtida por
plot(rede)

Podemos ver que a visualização está bastante suja. Para melhorarmos seu aspecto, vamos retirar os labels dos vértices e diminuir seu tamanho para 5.
plot(rede, vertex.label=NA, vertex.size=5)
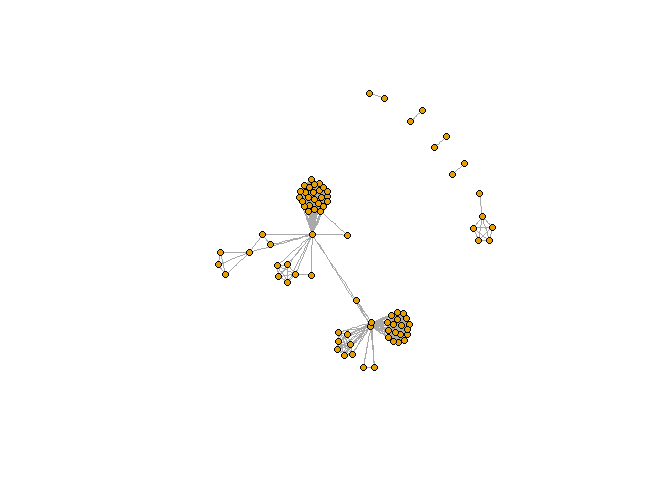
Podemos selecionar alguns layouts para a rede como os famosos algoritmos Kamada-Kawai, Fruchterman-Reingold ou o modelo circular, por exemplo.
plot(rede, vertex.label=NA, vertex.size=5, layout=layout_with_kk(rede), main="Kamada-Kawai")
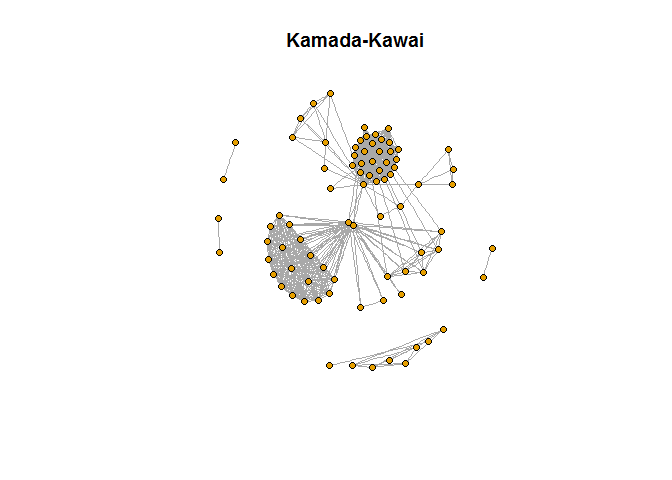
plot(rede, vertex.label=NA, vertex.size=5, layout=layout_with_fr(rede), main="Fruchterman-Reingold")
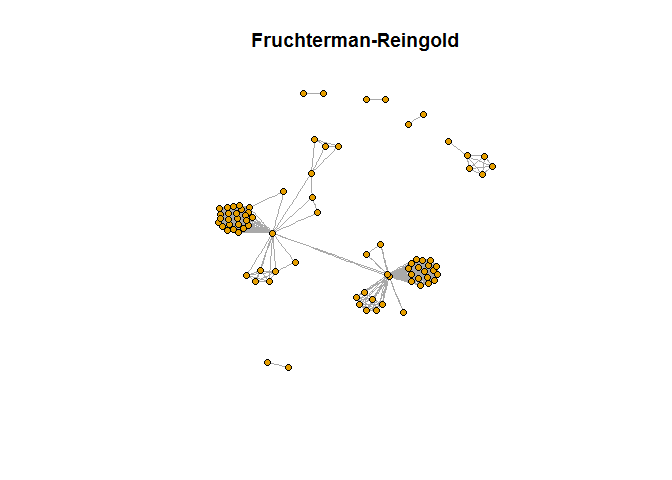
plot(rede, vertex.label=NA, vertex.size=5, layout=layout_in_circle(rede), main="Circle")
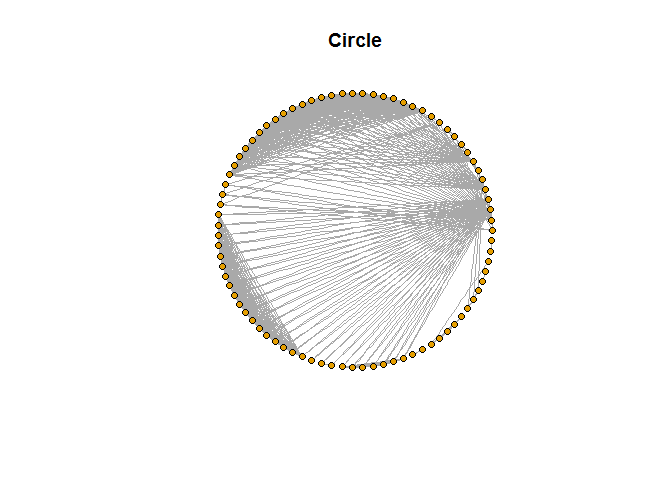
Medidas Descritivas
Para obter a lista de edges da rede, podemos usar o comando
E(rede)
## + 602/602 edges (vertex names):
## [1] Isabela Crepalde--Sarah Crepalde
## [2] Isabela Crepalde--Tânia R. Costa
## [3] Isabela Crepalde--Sueli Crepalde
## [4] Isabela Crepalde--Gabriela Crepalde
## [5] Isabela Crepalde--João Pedro Batista
## [6] Sarah Crepalde --Guilherme Castro
## [7] Sarah Crepalde --Avelar Junior
## [8] Sarah Crepalde --Ismael Luz
## [9] Sarah Crepalde --Eduardo
## [10] Sarah Crepalde --Nilton Morais
## + ... omitted several edges
Para obter a matriz de adjacências, use
matriz <- get.adjacency(rede)
Para obter o grau para cada vértice, use
grau <- degree(rede)
hist(grau, col="green", main="Degree")
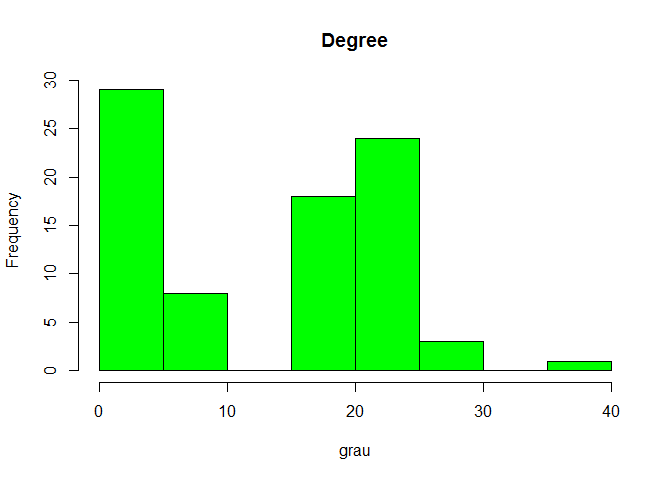
summary(grau)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.00 4.00 19.00 14.51 25.00 36.00
Para observar os vértices com maior ou menor grau, use
sort(grau, decreasing = T)
Para verificar a distribuição de grau, use
dd <- degree_distribution(rede)
O comando degree_distribution nos dá um vetor numérico indicando a frequência relativa de vértices com cada grau a partir do grau 0. Para verificar, por exemplo, a frequência relativa de vértices com grau 4, usamos
dd[5]
## [1] 0.04819277
Para plotar a distribuição de grau numa escala log-log, podemos usar
dist.grau <- degree.distribution(rede)
d <- 1:max(grau)-1
ind <- grau !=0
plot(d[ind], dist.grau[ind], log="xy", pch=19,
xlab=c("Log-Degree"), ylab=c("Log-Intensity"), main="Log-Log Degree Distribution")
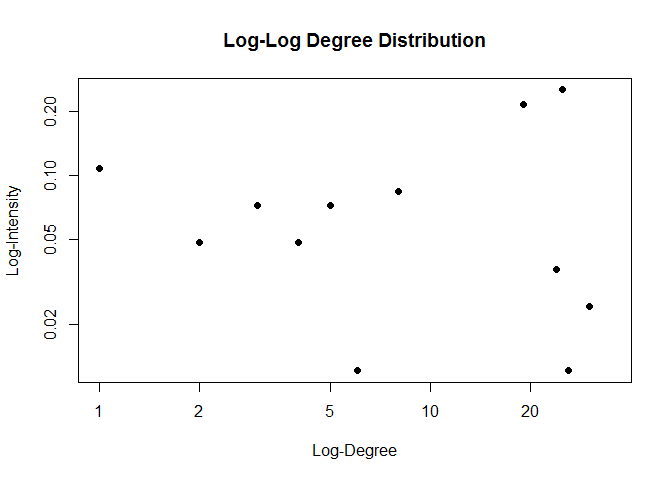
Para medidas de centralidade, use
inter <- betweenness(rede, directed=F)
hist(inter, col="lightblue", main="Betweeness")
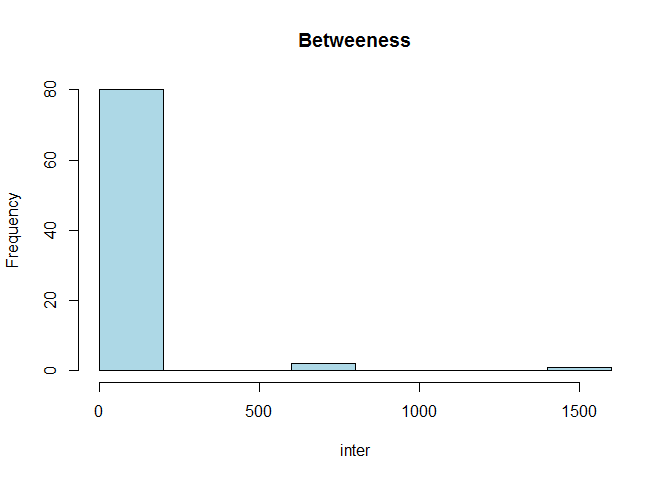
close <- closeness(rede)
hist(close, col="pink", main="Closeness")
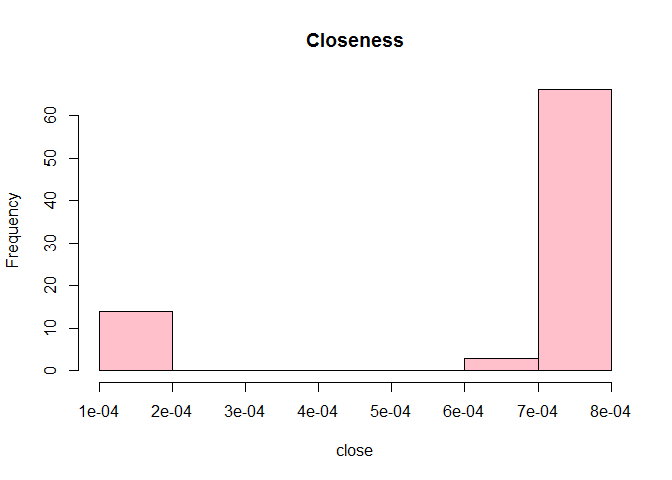
Para medidas da rede como densidade, diâmetro, distância média e algumas outras (observe que colocamos o parâmetro unconnected=TRUE porque esse é o caso. Se sua rede é toda conectada, use unconnected=FALSE), use:
graph.density(rede)
## [1] 0.1769027
diameter(rede, directed = F, unconnected = T)
## [1] 5
distance_table(rede, directed=F)
## $res
## [1] 602 583 1065 115
##
## $unconnected
## [1] 1038
mean_distance(rede, directed = F, unconnected = T)
## [1] 2.293023
distances(rede, v=V(rede)[3], to=V(rede)[11], mode="all")
## Joanir Oliveira
## Guilherme Castro 2
const <- constraint(rede)
hist(const, col="red", main="Constraint")
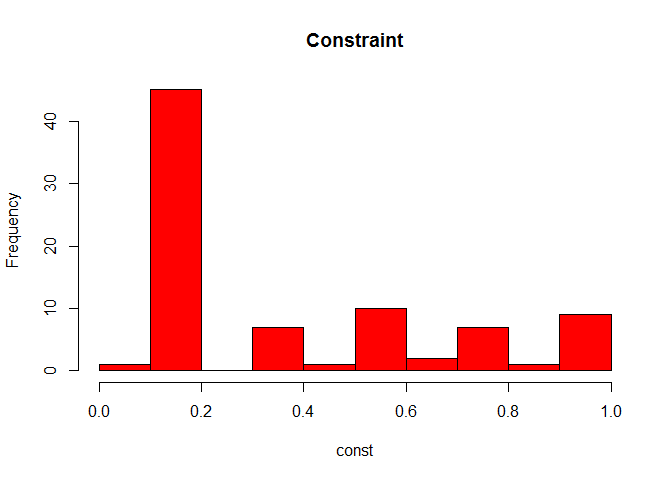
Vamos plotar novamente com algumas medidas extraídas e com cores diferentes.
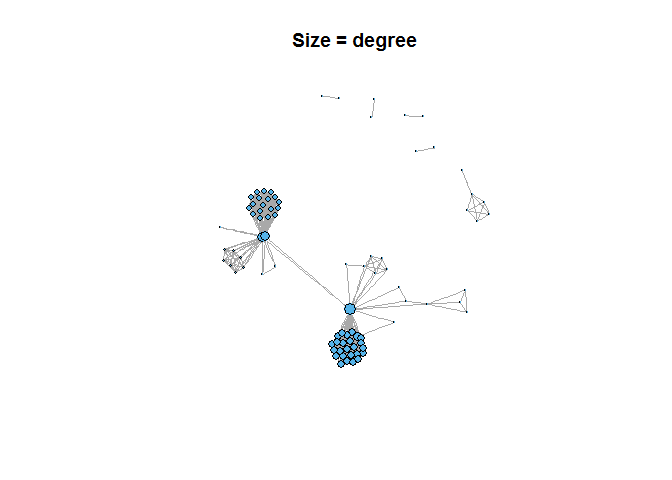
plot(rede, vertex.label=NA, vertex.color=2, vertex.size=grau/4, main="Size = degree")
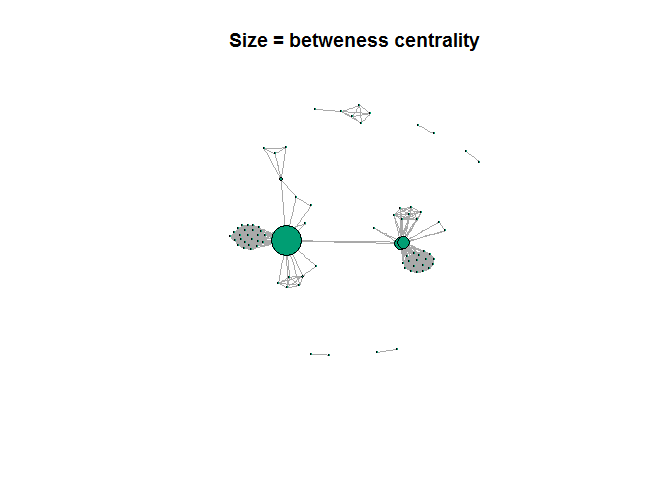
plot(rede, vertex.label=NA, vertex.color=3, vertex.size=inter/60, main="Size = betweness centrality")
plot(rede, vertex.label=NA, vertex.color=4, vertex.size=close*5000, main="Size = closeness centrality")

plot(rede, vertex.label=NA, vertex.color=5, vertex.size=const*10, main="Size = constraint")
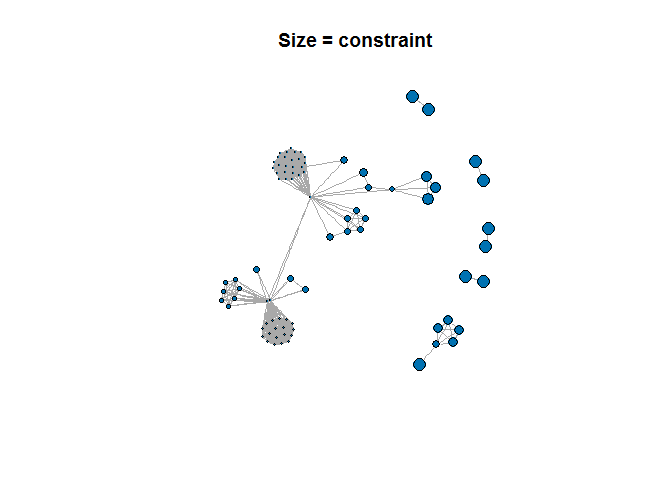
Para quem que não tem muita familiaridade com as medidas descritivas de redes, quero recomendar o livro dos professores Lazega e Higgins que está disponível tanto no site da editora Fino Traço quanto na Amazon. Além das medidas descritivas, o livro aborda a concepção de um estudo relacional e, em seu capítulo final, apresenta os últimos avanços em modelos estatísticos em redes.

Se tiverem dúvidas sobre algum código ou alguma dúvida específica sobre a rede em que estiverem trabalhando em suas pesquisas pessoais de tese e dissertação, deixem aqui seus comentários que tentarei responder o mais breve possível.
Obrigado!!
Referências
Csardi G, Nepusz T (2006). The igraph software package for complex network research, InterJournal, Complex Systems 1695. http://igraph.org
Lazega, Emmanuel; Higgins, Silvio S. (2015) Redes Sociais e Estruturas Relacionais. Belo Horizonte: Editora Fino Traço.
R Core Team (2016). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL https://www.R-project.org/