Estudando ERGMs, esbarrei neste excelente tutorial o qual traduzi para disponibilizá-lo à comunidade de língua portuguesa. A tradução conta com a autorização do autor, David Masad. A partir daqui, as linhas são dele! ;)

Este é um combinado de dois tutoriais: ERGM tutorial using the Grey’s Anatomy hookup network de Benjamin Lind e este tutorial sobre ERGMs using PyMC (o qual não sei quem escreveu). O que eu queria fazer era replicar o último tutorial com um dataset diferente, para ter certeza que eu entendi bem o que estava acontecendo. Estou compartilhando isto no caso de alguém achar útil.

Para uma explicação mais detalhada dos ERGMs, dê uma olhada nos tutoriais acima ou no meu tutorial on implementing ERGMs from scratch in Python (no final tem uma boa rodada de papers para leitura posterior).

Para mais sobre PyMC, você pode olhar o excelente handbook gratuito Bayesian Methods for Hackers de Cam Davidson-Pilon.

No momento da tradução deste post, as bibliotecas funcionam apenas com Python 3.6

import numpy as np
from scipy.special import comb
from itertools import product
import pymc
import networkx as nx
import matplotlib.pyplot as plt

Importando os dados

Infelizmente os dados do tutorial original sobre Grey’s Anatomy estão offline. Felizmente eles foram preservados neste Github por Alex Leavitt e Joshua Clark.

Os dados vêm em duas tabelas: a tabela de adjacência nos dá o grafo em si, e a tabela de atributos dos nós nos dá informações no nível dos nós de cada personagem. Abaixo, vamos importar as duas tabelas para o NetworkX.

Importando a matriz de adjacências

O NetworkX não possui um loader nativo para uma matriz de adjacência com nomes de linhas e colunas. Portanto, vamos importá-la manualmente. Primeiro, pegamos a primeira linha que nos diz quantos nós existem. Vamos utilizar essa linha para colocar os labels.

O primeiro comando utiliza o método wget para baixar os dados do repositório. Em seguida vamos movê-los para a pasta data. Lembre-se de que esses comandos só funcionam assim em Jupyter Notebook. Se estiver utilizando uma IDE, pode executá-los no terminal sem a !.

!wget https://raw.githubusercontent.com/alexleavitt/SNAinRworkshop/master/grey_adjacency.tsv

--2019-12-14 14:52:47--  https://raw.githubusercontent.com/alexleavitt/SNAinRworkshop/master/grey_adjacency.tsv
Resolving raw.githubusercontent.com (raw.githubusercontent.com)... 151.101.92.133
Connecting to raw.githubusercontent.com (raw.githubusercontent.com)|151.101.92.133|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 4470 (4,4K) [text/plain]
Saving to: 'grey_adjacency.tsv'

     0K ....                                                  100% 17,6K=0,2s

2019-12-14 14:52:47 (17,6 KB/s) - 'grey_adjacency.tsv' saved [4470/4470]

!mv grey_adjacency.tsv ../data

with open('../data/grey_adjacency.tsv') as f:
    first_line = f.readline()

print(first_line)

	addison	adele	altman	amelia	arizona	ava	avery	bailey	ben	burton	catherine	chief	colin	denny	derek	ellis grey	finn	grey	hahn	hank	izzie	karev	kepner	lexi	lloyd	lucy	megan	mostow	mrs. seabury	nancy	olivia	o'malley	owen	perkins	pierce	preston	reed	sloan	steve	susan grey	thatch grey	torres	tucker	yang

len(first_line.split('\t'))

45

Há 45 entradas separadas por tab na primeira linha incluindo o primeiro registro que está vazio (os labels das linhas começam embaixo desse espaço). Na verdade são 44 personagens na matriz.

Agora que já sabemos quantas linhas temos, podemos importar a matriz para NumPy, pulando a primeira linha e a primeira coluna:

adj = np.loadtxt('../data/grey_adjacency.tsv', delimiter='\t', skiprows=1, usecols=list(range(1,45)))

adj.shape

(44, 44)

Depois, vamos transformar a matriz de adjacências em uma rede. Vamos convertê-la em um objeto network e renomear os nós baseado nos headers das colunas.

G = nx.from_numpy_matrix(adj)

names = [name.strip() for name in first_line.split('\t')[1:]]

G = nx.relabel_nodes(G, {i: names[i] for i in range(44)})

Importando os atributos

Os dados de atributos estão em uma tabela convencional: cada linha é um personagem e cada coluna um atributo do personagem (veja o tutorial original para mais informações sobre a origem desses dados).

Usando o módulo csv podemos ler todas as linhas como dicionários, o que torna simples juntar os atributos à rede.

!wget https://raw.githubusercontent.com/alexleavitt/SNAinRworkshop/master/grey_nodes.tsv

--2019-12-14 14:52:47--  https://raw.githubusercontent.com/alexleavitt/SNAinRworkshop/master/grey_nodes.tsv
Resolving raw.githubusercontent.com (raw.githubusercontent.com)... 151.101.92.133
Connecting to raw.githubusercontent.com (raw.githubusercontent.com)|151.101.92.133|:443... connected.
HTTP request sent, awaiting response... 200 OK
Length: 1692 (1,7K) [text/plain]
Saving to: 'grey_nodes.tsv'

     0K .                                                     100% 4,70M=0s

2019-12-14 14:52:47 (4,70 MB/s) - 'grey_nodes.tsv' saved [1692/1692]

!mv grey_nodes.tsv ../data

import csv

node_attributes = []
with open('../data/grey_nodes.tsv') as f:
    reader = csv.DictReader(f, dialect=csv.excel_tab)
    for row in reader:
        node_attributes.append(row)

Checando:

node_attributes[0]

OrderedDict([('name', 'addison'),
             ('sex', 'F'),
             ('race', 'White'),
             ('birthyear', '1967'),
             ('position', 'Attending'),
             ('season', '1'),
             ('sign', 'Libra')])

Agora vamos juntar os atributos com cada nó pelos nomes:

for node in node_attributes:
    name = node['name']
    for key, val in node.items():
        if key == 'name':
            continue
        G.nodes[name][key] = val

# Checking
G.nodes['addison']

{'sex': 'F',
 'race': 'White',
 'birthyear': '1967',
 'position': 'Attending',
 'season': '1',
 'sign': 'Libra'}

Plotando o grafo de relacionamentos

Agora que temos os dados devidamente importados, vamos plotar o grafo de relacionamentos (hookup).

colors = {'M': 'mediumslateblue', 'F': 'hotpink'}
node_colors = [colors[node[1]['sex']] for node in G.nodes(data=True)]

pos = nx.spring_layout(G, k=0.3, scale=2)
fig, ax = plt.subplots(figsize=(10,10))
nx.draw_networkx_nodes(G, pos, node_size=100, node_color=node_colors, ax=ax)
nx.draw_networkx_edges(G, pos, alpha=0.5, ax=ax)
nx.draw_networkx_labels(G, pos, ax=ax)

#ax.set_xlim(-0.25, 4.25)
#ax.set_ylim(-0.25, 4.25)
#_ = ax.axis('off')
plt.show()

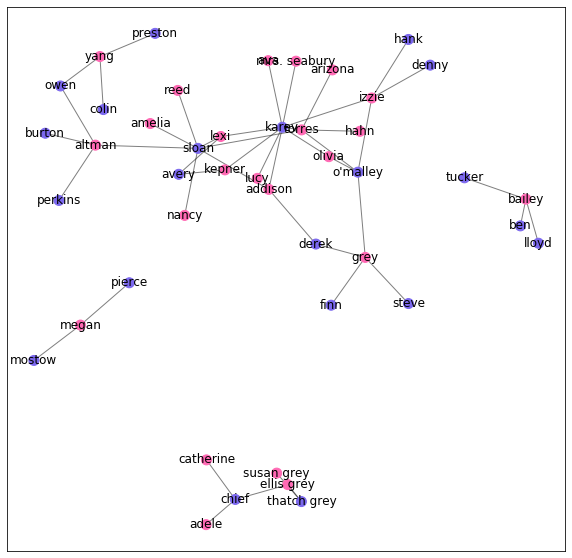
Construindo o ERGM

Agora chegamos à parte central: construir e estimar um ERGM com PyMC.

Para começar, precisamos saber que modelo estamos estimando de fato. Vou usar o mais simples, explicando a rede em termos do número de laços e se os laços são entre nós do mesmo gênero.

Precisamos de 2 matrizes $n \times n$, uma para cada estatística da rede (parâmetro). Cada célula em cada matriz indica como a presença daquele laço potencial mudaria a estatística mantendo-se todo o restante da rede constante.

Para a contagem de laços (edge count) a matriz precisa conter apenas 1s - já que qualquer novo laço, por definição incrementa a contagem por 1.

Matching de gênero é um exemplo específico de matching de atributos: queremos uma matriz $M$ tal que $m_{i, j} = 1$ se os nós i e j tem o mesmo valor de atributo (no caso o gênero), senão, 0.

Agora aqui está uma mudança que faremos do tutorial original. Diferente da prison friendship network, o grafo de relacionamento é não direcionado - se i ficou com j, então obviamente j ficou com i. Isso significa que nós precisamos mesmo somente da metade da matriz, seja a metade superior ou inferior. Podemos zerar a outra metade para ter certeza de que contamos apenas um laço por díade.

def edge_count(G):
    size = len(G)
    ones = np.ones((size, size))
    # Zero out the upper triangle
    if not G.is_directed():
        ones[np.triu_indices_from(ones)] = 0
    return ones

def node_match(G, attrib):
    size = len(G)
    attribs = [node[1][attrib] for node in G.nodes(data=True)]
    match = np.zeros(shape=(size, size))
    for i in range(size):
        for j in range(size):
            if i != j and attribs[i] == attribs[j]:
                match[i,j] = 1
    if not G.is_directed():
        match[np.triu_indices_from(match)] = 0
    return match

# Cria a matriz de match de gênero
gender_match_mat = node_match(G, 'sex')

Agora vamos trazer ao PyMC variáveis estocásticas para os coeficientes em ambas as matrizes de estatísticas. O início para elas pode ser arbitrário, mas queremos que elas sejam capazes de receber qualquer valor, negativo ou positivo, e sejam centradas em 0. Então, optamos por uma distribuição normal.

O termo de fato para cada estatística é o coeficiente vezes a matriz; visto que esses valores são completamente independentes em variáveis estocásticas, elas são variáveis determinísticas no PyMC.

density_coef = pymc.Normal('density', 0, 0.001)
gender_match_coef = pymc.Normal('gender_match', 0, 0.001)

density_term = density_coef * edge_count(G)
gender_match_term = gender_match_coef * gender_match_mat

term_list = [density_term, gender_match_term]

Agora vamos criar a matriz de probabilidade onde $P_{i, j}$ é a probabilidade de um laço entre i e j. Isso é outra variável determinística do PyMC visto que a probabilidade é baseada nos dois termos definidos acima.

Definimos o triângulo superior da matriz como 0 aqui para que haja somente uma probabilidade associada a cada díade.

@pymc.deterministic
def probs(term_list=term_list):
    probs = 1 / (1 + np.exp(-1 * sum(term_list))) # A função logística
    probs[np.diag_indices_from(probs)] = 0
    # Cortar manualmente metade da matriz
    probs[np.triu_indices_from(probs)] = 0
    return probs

[[0.5 0.5 0.5 ... 0.5 0.5 0.5]
 [1.  0.5 0.5 ... 0.5 0.5 0.5]
 [1.  1.  0.5 ... 0.5 0.5 0.5]
 ...
 [1.  1.  1.  ... 0.5 0.5 0.5]
 [1.  1.  1.  ... 1.  0.5 0.5]
 [1.  1.  1.  ... 1.  1.  0.5]]

Finalmente, vamos criar as variáveis resposta: trata-se de uma matriz de Bernoulli (Bernoulli random values), uma para cada laço potencial, realizada com a probabilidade determinada por nosso modo. Essa matriz é na verdade observada como a matriz de adjacência da rede. É para esta resposta que PyMC vai maximizar a probabilidade do modelo.

# Pega a matriz de adjacência e zera o triângulo superior
matrix = nx.to_numpy_matrix(G)
matrix[np.triu_indices_from(matrix)] = 0

outcome = pymc.Bernoulli('outcome', probs, value=matrix, observed=True)

Para ver as redes de amostra geradas pela distribuição posterior, adicionamos uma variável aleatória: um outcome simulado. Ele tem a mesma forma da matriz de outcome acima mas não é declarada como observada. Ao invés disso, o valor de cadad laço potencial será aleatoriamente desenhado baseado na matriz de probabilidades.

sim_outcome = pymc.Bernoulli('sim_outcome', probs)

Estimando o modelo

Com todas as variáveis finalmente definidas, podemos plugar todas no objeto do modelo e começar o processo de MCMC.

modelo = pymc.Model([outcome, sim_outcome, probs, density_coef, density_term,
                    gender_match_coef, gender_match_term])

mcmc = pymc.MCMC(modelo)
mcmc.sample(50000, 1000, 50)

C:\Users\Neylson\Anaconda3\envs\networks\lib\site-packages\pymc\MCMC.py:81: UserWarning: Instantiating a Model object directly is deprecated. We recommend passing variables directly to the Model subclass.
  warnings.warn(message)


 [-----------------100%-----------------] 50000 of 50000 complete in 20.7 sec

density_trace = mcmc.trace("density")[:]
gender_match_trace = mcmc.trace("gender_match")[:]

print("Density: {0:.3f}, {1:.3f}".format(np.mean(density_trace), np.std(density_trace)))
print("Gender: {0:.3f}, {1:.3f}".format(np.mean(gender_match_trace), np.std(gender_match_trace)))

Density: -2.308, 0.159
Gender: -3.395, 0.807

Isso está bem próximo dos coeficientes e erros padrão computados em R, sugerindo que o modelo foi especificado e estimado corretamente.

Diagnóstico

O pacote ergm do R nos permite plotar alguns gráficos de diagnóstico automaticamente, nos ajudando a ter certeza de o modelo não se degenerou e que a cadeia está indo bem. Faremos gráficos similares aqui:

fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(221)
ax1.plot(density_trace)
ax1.set_title("Density")
ax2 = fig.add_subplot(222)
ax2.hist(density_trace)
ax2.set_title('Density')

ax3 = fig.add_subplot(223)
ax3.plot(gender_match_trace)
ax3.set_title("Gender Match")
ax4 = fig.add_subplot(224)
ax4.hist(gender_match_trace)
ax4.set_title('Gender Match')

Text(0.5, 1.0, 'Gender Match')

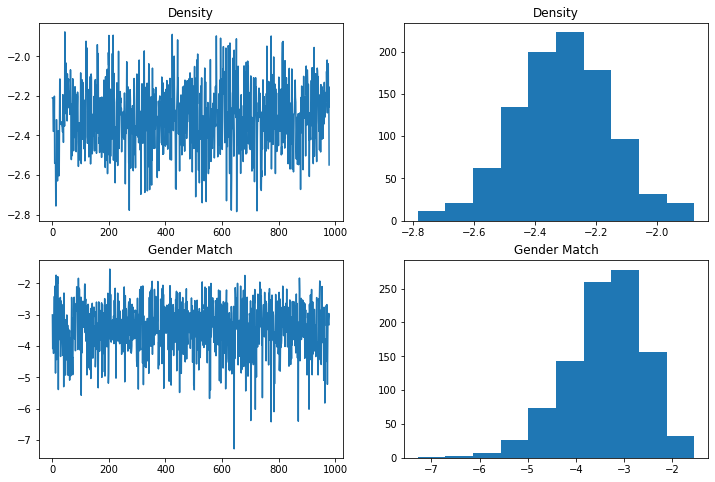
Checando o GOF (Goodness of Fit)

Um meio de inspecionar a qualidade do ajuste (GOF - Goodness of Fit) do modelo é tirar uma realização aleatória da rede da distribuição posterior e ver como ela se compara à rede observada. Isto é uma das coisas que podemos fazer com a variável sim_outcome que adicionamos ao modelo.

realization = mcmc.trace('sim_outcome')[-1] # pega a última

Ou podemos fixar os parâmetros e desenhar aleatoriamente:

#density_coef.value = np.mean(density_trace)
#gender_match_coef.value = np.mean(gender_match_trace)
#realization = sim_outcome.random()

Convertemos a matriz realizada para uma redee adicionamos os atributos:

sim_g = nx.from_numpy_matrix(realization)
sim_g = nx.relabel_nodes(sim_g, {i: names[i] for i in range(44)})
for node in node_attributes:
    name = node['name']
    for key, val in node.items():
        if key == "name":
            continue
        sim_g.nodes[name][key] = val

E visualizamos. Não nos importamos com os indivíduos específicos aqui já que nosso modelo estava buscando apenas por matching de gênero.

colors = {'M': 'mediumslateblue', 'F': 'hotpink'}
node_colors = [colors[node[1]['sex']] for node in sim_g.nodes(data=True)]

pos = nx.spring_layout(sim_g, k=0.3, scale=3)
fig, ax = plt.subplots(figsize=(10,10))
nx.draw_networkx_nodes(sim_g, pos, node_size=100, node_color=node_colors, ax=ax)
nx.draw_networkx_edges(sim_g, pos, alpha=0.5, ax=ax)
#nx.draw_networkx_labels(sim_g, pos, ax=ax)

#ax.set_xlim(-0.25, 4.25)
#ax.set_ylim(-0.25, 4.25)
#_ = ax.axis('off')
plt.show()

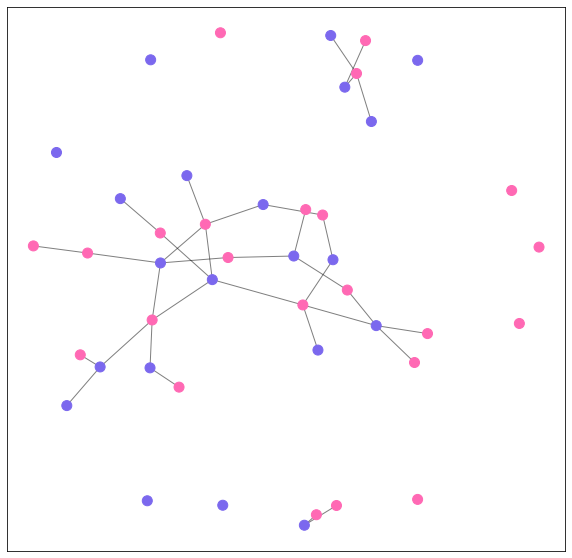
O grafo parece “bem certinho” no olho (uma verificação SUUUPER científica…) e o modelo parece capturar bem a tendência de pareamentos heterossexuais (embora haja pares homossexuais na rede simulada). Aqui há mais gente sozinha do que na rede observada - embora a mesma quantidade seja também produzida pelo modelo em R.

Distribuição de grau

Outro modo de verificar o GOF é comparar a distribuição de grau da rede simulada e da rede observada. O pacote ergm já possui essa feature mas aqui vamos implementá-la.

Para fazer isso, vamos contar o número de nós de cada grau na rede observada e na rede simulada e plotá-los juntos.

from collections import defaultdict, Counter

A distribuição da rede observada:

obs_deg_freq = Counter(dict(nx.degree(G)).values())
x = list(obs_deg_freq.keys())
y = list(obs_deg_freq.values())

A distribuição da rede simulada:

deg_freq = defaultdict(list)

# Não vamos nos preocupar com propriedades dos nós agora, apenas o grau
for realization in mcmc.trace('sim_outcome')[:]:
    sim_g = nx.from_numpy_matrix(realization)
    for deg, count in Counter(dict(nx.degree(sim_g)).values()).items():
        deg_freq[deg].append(count)

vals = list(deg_freq.values())
labels = list(deg_freq.keys())

E finalmente, o plot: pontos pretos para a contagem de graus observada, box-and-whiskers plot para as distribuições:

fig, ax = plt.subplots()

h = ax.boxplot(vals, positions=labels)
ax.scatter(x, y, s=40)
#ax.plot(x, y)
ax.set_xlim(-1, 10.5)
ax.set_ylim(0,30)
ax.set_xticklabels(labels)
ax.set_xlabel('Degree')
ax.set_ylabel("Frequency")
ax.set_title("Degree Distribution\nObserved vs Simulated")

Text(0.5, 1.0, 'Degree Distribution\nObserved vs Simulated')

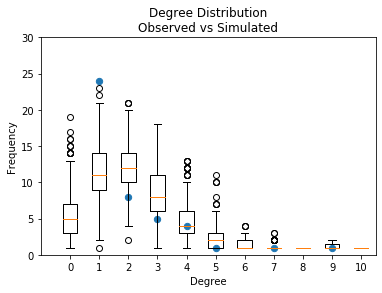
Como podemos ver, houve muito mais solteiros simulados do que no modelo observado e menos nós monogâmicos (grau 1 neste caso). Mais importante, para nossos propósitos, isto está bem parecido com os resultados produzidos pelo modelo em R!