Olá! Em nosso post anterior inspirado no artigo de Riebling e Schmitz (2016) intitulado ZombieApocalypse: Modeling the social dynamics of infection and rejection, apresentamos uma solução para a implementação de um modelo de contágio ou modelo de difusão em rede simulando uma infestação zumbi. Hoje, vamos continuar o mesmo trabalho mas agora vamos simular mais dois cenários diferentes. Além disso, vamos investigar também a dinâmica da rede ao longo do processo de contágio. Para isso estamos usando a distro Anaconda do Python 3.5. No post anterior apresento as bibliotecas que precisam ser instaladas. Vamos lá!

Carregando bibliotecas
import matplotlib.pyplot as plt
import networkx as nx
import pandas as pd
import numpy as np
import seaborn as sns
import random
import os
from nxsim import NetworkSimulation, BaseNetworkAgent, BaseLoggingAgent
sns.set_context('notebook')
os.chdir('/home/neylson/diffusion_model')
Algumas funções úteis
def census_to_df(log, num_trials=1, state_id=1, dir_path='sim_01'):
"""Reads nxsim log files and returns the sum of agents with a given state_id at
every time interval of the simulation for every run of the simulation as a pandas
DataFrame object."""
D = {}
for i in range(num_trials):
name = 'Trial ' + str(i)
trial = log.open_trial_state_history(dir_path=dir_path,
trial_id=i)
census = [sum([1 for node_id, state in g.items()
if node_id != 'topology' and state['id'] == state_id])
for t, g in trial.items()]
D[name] = census
return pd.DataFrame(D)
def friends_to_the_end(log, num_trials=1, dir_path='sim_01'):
"""Reads nxsim log files and returns the number of human friends connected
to every human at every time interval of the simulation for every run of
the simulation as a pandas DataFrame object."""
D = {}
for i in range(num_trials):
name = 'Trial ' + str(i)
trial = log.open_trial_state_history(dir_path=dir_path,
trial_id=i)
friends = [np.mean([state['friends'] for node_id, state in g.items()
if node_id != 'topology' and state['id'] == 0])
for t, g in trial.items()]
D[name] = friends
return pd.DataFrame(D)
Estabelecendo a topologia
Vamos estabelecer novamente uma rede livre de escala de 100 nós onde as interações vão acontecer.
number_of_nodes = 100
G = nx.scale_free_graph(number_of_nodes).to_undirected()
Novos cenários
O cenário básico já foi implementado no post anterior. Vamos retomar o segundo cenário, Escape, onde cada nó, ao reconhecer um vizinho zumbi, tem a chance de escapar e “cortar” o laço com ele. Ao código original, adicionei apenas uma contagem para cada rodada de quantos laços foram cortados (isso será importante na investigação posterior da dinâmica da rede) e uma função que coleta as relações de cada nó em cada rodada. Vamos ao código.
class ZombieEscape(BaseNetworkAgent):
def __init__(self, environment=None, agent_id=0, state=()):
super().__init__(environment=environment, agent_id=agent_id, state=state)
self.inf_prob = 0.3
self.run_prob = 0.1
def run(self):
while True:
if self.state['id'] == 0:
self.run_you_fools()
self.check_for_infection()
self.count_friends()
self.get_net()
yield self.env.timeout(1)
else:
yield self.env.event()
def run_you_fools(self):
zombie_neighbors = self.get_neighboring_agents(state_id=1)
for neighbor in zombie_neighbors:
if random.random() < self.run_prob:
self.global_topology.remove_edge(self.id, neighbor.id)
self.state['removed'] = (self.id, neighbor.id)
print('Rejection:', self.env.now, 'Edge:', self.id, neighbor.id, sep='\t')
def check_for_infection(self):
zombie_neighbors = self.get_neighboring_agents(state_id=1)
for neighbor in zombie_neighbors:
if random.random() < self.inf_prob:
self.state['id'] = 1 # zombie
print('Infection:', self.env.now, self.id, '<--', neighbor.id, sep='\t')
break
def count_friends(self):
human_neighbors = self.get_neighboring_agents(state_id=0)
self.state['friends'] = len(human_neighbors)
def get_net(self):
nodes = self.get_neighboring_nodes()
self.state['topology'] = nodes
Agora vamos programar dois novos cenários, Sentimentality e Stigma.
Zombie Sentimentality
Este cenário baseia-se no velho dilema de ter que matar um amigo que acabou de ser mordido e que inevitavelmente se transformará num zumbi. Segundo os autores do artigo, as tramas com zumbis normalmente confrontam uma sociedade condenada com suas escolhas morais. Numa sociedade onde acontece um apocalipse zumbi, a compaixão é colocada em oposição à sobrevivência. Neste cenário, escapar torna-se mais difícil por causa do laço afetivo entre as pessoas. Vamos ao código.
class ZombieSentimentality(BaseNetworkAgent):
def __init__(self, environment=None, agent_id=0, state=()):
super().__init__(environment=environment, agent_id=agent_id, state=state)
self.inf_prob = 0.3
self.run_prob = 0.1
self.sent_coef = 0.05
def run(self):
while True:
if self.state['id'] == 0:
self.check_for_sentimentality()
self.check_for_infection()
self.count_friends()
yield self.env.timeout(1)
else:
yield self.env.event()
def check_for_infection(self):
zombie_neighbors = self.get_neighboring_agents(state_id=1)
for neighbor in zombie_neighbors:
if random.random() < self.inf_prob:
self.state['id'] = 1 # zombie
print('Infection:', self.env.now, self.id, '<--', neighbor.id, sep='\t')
break
def check_for_sentimentality(self):
zombie_neighbors = self.get_neighboring_agents(state_id=1)
sent_prob = self.run_prob - (self.env.now * self.sent_coef)
for neighbor in zombie_neighbors:
if random.random() < sent_prob:
self.global_topology.remove_edge(self.id, neighbor.id)
print('Rejection:', self.env.now, 'Edge:', self.id, neighbor.id, sep='\t')
def count_friends(self):
human_neighbors = self.get_neighboring_agents(state_id=0)
self.state['friends'] = len(human_neighbors)
Vamos rodar agora as duas simulações e compará-las.
# Simulação ZombieEscape
# Starting out with a human population
init_states = [{'id': 0, } for _ in range(number_of_nodes)]
# Randomly seeding patient zero
patient_zero = random.randint(0, number_of_nodes)
init_states[patient_zero] = {'id': 1}
# Setting up the simulation
sim = NetworkSimulation(topology=G, states=init_states, agent_type=ZombieEscape,
max_time=28, num_trials=100, logging_interval=1.0, dir_path='sim_02')
# Running the simulation
sim.run_simulation()
# Simulação ZombieSentimentality
# Starting out with a human population
init_states = [{'id': 0, } for _ in range(number_of_nodes)]
# Randomly seeding patient zero
patient_zero = random.randint(0, number_of_nodes)
init_states[patient_zero] = {'id': 1}
# Setting up the simulation
sim = NetworkSimulation(topology=G, states=init_states, agent_type=ZombieSentimentality,
max_time=28, num_trials=100, logging_interval=1.0, dir_path='sim_03')
# Running the simulation
sim.run_simulation()
Starting simulations...
---Trial 0---
Setting up agents...
Rejection: 0 Edge: 20 68
Written 28 items to pickled binary file: sim_02/log.0.state.pickled
---Trial 1---
Setting up agents...
Infection: 1 20 <-- 68
Infection: 1 54 <-- 20
Infection: 1 59 <-- 20
Rejection: 1 Edge: 76 20
Infection: 1 86 <-- 54
Infection: 1 91 <-- 20
Infection: 2 0 <-- 54
..........................
Infection: 8 72 <-- 0
Infection: 8 88 <-- 0
Infection: 8 96 <-- 1
Infection: 8 99 <-- 27
Infection: 9 38 <-- 19
Infection: 9 60 <-- 1
Infection: 9 67 <-- 4
Infection: 9 89 <-- 23
Infection: 10 35 <-- 0
Infection: 12 64 <-- 1
Written 28 items to pickled binary file: sim_03/log.99.state.pickled
Simulation completed.
Vamos plotar agora o resultado final de Humanos X Zumbis para o cenário Escape e para o cenário Sentimentality comparando-o com o anterior.
zombies = census_to_df(BaseLoggingAgent, 100, 1, dir_path='sim_02').T
humans = census_to_df(BaseLoggingAgent, 100, 0, dir_path='sim_02').T
## For later comparisons:
mean_escape_zombies = zombies.mean()
mean_escape_humans = humans.mean()
plt.plot(zombies.mean(), color='b')
plt.fill_between(zombies.columns, zombies.max(), zombies.min(), color='b', alpha=.2)
plt.plot(humans.mean(), color='g')
plt.fill_between(humans.columns, humans.max(), humans.min(), color='g', alpha=.2)
plt.title('Escape ZombieApokalypse, $P_{inf} = 0.3$, $P_{run} = 0.1$')
plt.legend(['Zombies', 'Humans'], loc=7, frameon=True)
plt.xlim(xmax=27)
plt.xticks(np.arange(0, 28., 3), tuple(range(1, 29, 3)))
plt.ylabel('Population')
plt.xlabel('Simulation time')
plt.show()
# plotting sentimentality
zombies = census_to_df(BaseLoggingAgent, 100, 1, dir_path='sim_03').T
humans = census_to_df(BaseLoggingAgent, 100, 0, dir_path='sim_03').T
plt.plot(zombies.mean(), color='r')
plt.plot(humans.mean(), color='y')
plt.plot(mean_escape_zombies, color='b')
plt.plot(mean_escape_humans, color='g')
plt.title('Sentimentality ZombieApokalypse, $P_{inf} = 0.3$, $P_{run} = 0.1$, $P_{sent} = 0.05$')
plt.legend(['"Sentimentality" Zombies', '"Sentimentality" Humans',
'"Escape" Zombies', '"Escape" Humans'],
loc=7, frameon=True)
plt.xlim(xmax=27)
plt.xticks(np.arange(0, 28., 3), tuple(range(1, 29, 3)))
plt.ylabel('Population')
plt.xlabel('Simulation time')
plt.show()
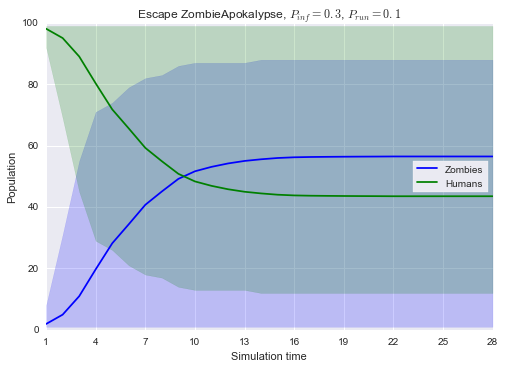
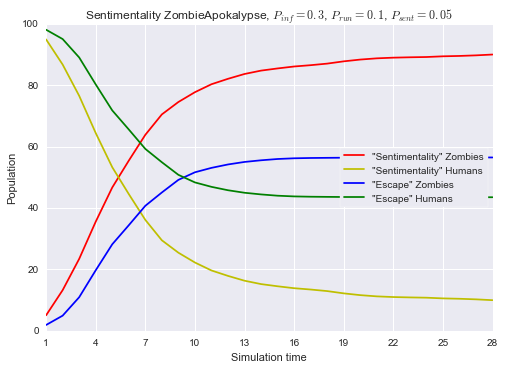
É visível que, neste caso, o prender-se a um humano mordido acarreta em maior sucesso da infestação zumbi. Agora, vamos considerar um quarto cenário, Stigma.
Zombie Stigma
Neste cenário os autores simulam o “deixar as presas fáceis para trás”. Isso, segundo Riebling e Schmitz (2016), pode ser visto como um indício da erosão da moralidade humana. Aqueles humanos são considerados “zombie snack” e só servem para atrasar o grupo são deixados para trás. Vamos ao código e às simulações.
class ZombieStigma(BaseNetworkAgent):
def __init__(self, environment=None, agent_id=0, state=()):
super().__init__(environment=environment, agent_id=agent_id, state=state)
self.inf_prob = 0.3
self.run_prob = 0.1
self.sent_coef = 0
self.stigma_coef = 0.02
def run(self):
while True:
if self.state['id'] == 0:
self.check_for_sentimentality()
self.stigmatize()
self.check_for_infection()
self.count_friends()
yield self.env.timeout(1)
else:
yield self.env.event()
def stigmatize(self):
human_neighbors = self.get_neighboring_agents(state_id=0)
for neighbor in human_neighbors:
sorrounding_zombies = neighbor.get_neighboring_agents(state_id=1)
if random.random() < (len(sorrounding_zombies) * self.stigma_coef):
self.global_topology.remove_edge(self.id, neighbor.id)
print('Stigmatize:', self.env.now, 'Edge:', self.id, neighbor.id, sep='\t')
def check_for_infection(self):
zombie_neighbors = self.get_neighboring_agents(state_id=1)
for neighbor in zombie_neighbors:
if random.random() < self.inf_prob:
self.state['id'] = 1 # zombie
print('Infection:', self.env.now, self.id, '<--', neighbor.id, sep='\t')
break
def check_for_sentimentality(self):
zombie_neighbors = self.get_neighboring_agents(state_id=1)
sent_prob = self.run_prob - (self.env.now * self.sent_coef)
for neighbor in zombie_neighbors:
if random.random() < sent_prob:
self.global_topology.remove_edge(self.id, neighbor.id)
print('Rejection:', self.env.now, 'Edge:', self.id, neighbor.id, sep='\t')
def count_friends(self):
human_neighbors = self.get_neighboring_agents(state_id=0)
self.state['friends'] = len(human_neighbors)
# Simulando a Stigmatization
# Starting out with a human population
init_states = [{'id': 0, } for _ in range(number_of_nodes)]
# Randomly seeding patient zero
patient_zero = random.randint(0, number_of_nodes)
init_states[patient_zero] = {'id': 1}
# Setting up the simulation
sim = NetworkSimulation(topology=G, states=init_states, agent_type=ZombieStigma,
max_time=28, num_trials=100, logging_interval=1.0, dir_path='sim_04')
# Running the simulation
sim.run_simulation()
Starting simulations...
---Trial 0---
Setting up agents...
Rejection: 0 Edge: 0 65
Written 28 items to pickled binary file: sim_04/log.0.state.pickled
---Trial 1---
Setting up agents...
Infection: 1 0 <-- 65
Rejection: 1 Edge: 2 0
Infection: 1 7 <-- 0
Rejection: 1 Edge: 10 0
Infection: 1 15 <-- 0
Infection: 1 21 <-- 0
Infection: 1 27 <-- 0
Infection: 1 28 <-- 15
Stigmatize: 1 Edge: 32 1
Infection: 1 33 <-- 0
Rejection: 1 Edge: 39 0
Rejection: 1 Edge: 48 0
Rejection: 1 Edge: 50 0
Infection: 1 66 <-- 0
Infection: 1 70 <-- 0
Stigmatize: 1 Edge: 74 13
Infection: 1 81 <-- 0
.........................
Rejection: 14 Edge: 99 27
Rejection: 15 Edge: 51 20
Rejection: 18 Edge: 32 1
Rejection: 18 Edge: 58 0
Rejection: 18 Edge: 90 1
Infection: 21 33 <-- 45
Written 28 items to pickled binary file: sim_04/log.99.state.pickled
Simulation completed.
Vamos agora plotar os resultados de Humanos X Zumbis dessa simulação.
# Zombie Stigmatization
zombies = census_to_df(BaseLoggingAgent, 100, 1, dir_path='sim_04').T
humans = census_to_df(BaseLoggingAgent, 100, 0, dir_path='sim_04').T
plt.plot(zombies.mean(), color='b')
plt.fill_between(zombies.columns, zombies.max(), zombies.min(), color='b', alpha=.2)
plt.plot(humans.mean(), color='g')
plt.fill_between(humans.columns, humans.max(), humans.min(), color='g', alpha=.2)
plt.title('Stigma ZombieApokalypse, $P_{inf} = 0.3$, $P_{run} = 0.1$, $P_{sti}=0.02$')
plt.legend(['Zombies', 'Humans'], loc=7, frameon=True)
plt.xlim(xmax=27)
plt.xticks(np.arange(0, 28., 3), tuple(range(1, 29, 3)))
plt.ylabel('Population')
plt.xlabel('Simulation time')
plt.show()
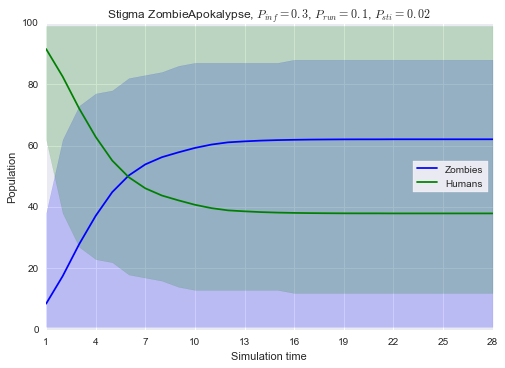
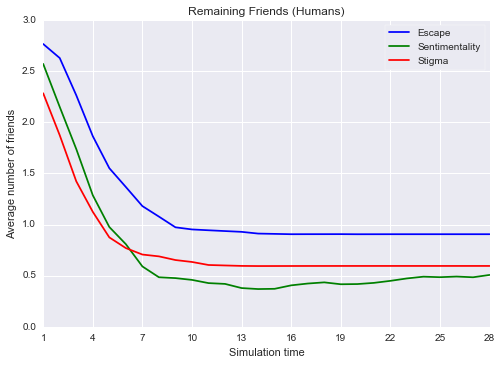
Agora, vamos comparar o número médio de amigos humanos em cada um dos três cenários aqui apresentados.
escape_friends = friends_to_the_end(BaseLoggingAgent, 100, dir_path='sim_02').T
sentimentality_friends = friends_to_the_end(BaseLoggingAgent, 100, dir_path='sim_03').T
stigma_friends = friends_to_the_end(BaseLoggingAgent, 100, dir_path='sim_04').T
plt.plot(escape_friends.mean(), color='b')
plt.plot(sentimentality_friends.mean(), color='g')
plt.plot(stigma_friends.mean(), color='r')
plt.title('Remaining Friends (Humans)')
plt.legend(['Escape', 'Sentimentality', 'Stigma'], loc='best', frameon=True)
plt.xlim(xmax=27)
plt.xticks(np.arange(0, 28., 3), tuple(range(1, 29, 3)))
plt.ylabel('Average number of friends')
plt.xlabel('Simulation time')
plt.show()
Investigando a dinâmica da rede
O cenário Escape pressupõe que os indivíduos, ao reconhecerem um zumbi, tenham a chance de escapar e romper seu laço com ele. Desse modo, podemos investigar a dinâmica da rede. Por isso, quando programamos os agentes, definimos um atributo de cada agente como “removidos” que guarda uma lista com os laços removidos de cada ator em cada rodada. Vamos resgatar esses laços agora e removê-los da rede inicial.
log = BaseLoggingAgent.open_trial_state_history(dir_path='sim_02', trial_id=8)
removidos = {}
for time in range(28):
print('Grafo no tempo '+str(time))
remov = []
for node in range(100):
try:
rem = log[time][node]['removed']
remov.append(rem)
print(rem)
except KeyError:
print('Sem removidos na rodada')
continue
removidos[time] = remov
pos = nx.fruchterman_reingold_layout(G)
G1 = nx.Graph(G)
G1.remove_edges_from(removidos[1])
G2 = nx.Graph(G)
G2.remove_edges_from(removidos[2])
G3 = nx.Graph(G)
G3.remove_edges_from(removidos[3])
G4 = nx.Graph(G)
G4.remove_edges_from(removidos[4])
G5 = nx.Graph(G)
G5.remove_edges_from(removidos[5])
G6 = nx.Graph(G)
G6.remove_edges_from(removidos[6])
G7 = nx.Graph(G)
G7.remove_edges_from(removidos[7])
G8 = nx.Graph(G)
G8.remove_edges_from(removidos[8])
G9 = nx.Graph(G)
G9.remove_edges_from(removidos[9])
G10 = nx.Graph(G)
G10.remove_edges_from(removidos[10])
G11 = nx.Graph(G)
G11.remove_edges_from(removidos[11])
G12 = nx.Graph(G)
G12.remove_edges_from(removidos[12])
G13 = nx.Graph(G)
G13.remove_edges_from(removidos[13])
G14 = nx.Graph(G)
G14.remove_edges_from(removidos[14])
G15 = nx.Graph(G)
G15.remove_edges_from(removidos[15])
G16 = nx.Graph(G)
G16.remove_edges_from(removidos[16])
G17 = nx.Graph(G)
G17.remove_edges_from(removidos[17])
G18 = nx.Graph(G)
G18.remove_edges_from(removidos[18])
G19 = nx.Graph(G)
G19.remove_edges_from(removidos[19])
G20 = nx.Graph(G)
G20.remove_edges_from(removidos[20])
G21 = nx.Graph(G)
G21.remove_edges_from(removidos[21])
G22 = nx.Graph(G)
G22.remove_edges_from(removidos[22])
G23 = nx.Graph(G)
G23.remove_edges_from(removidos[23])
G24 = nx.Graph(G)
G24.remove_edges_from(removidos[24])
G25 = nx.Graph(G)
G25.remove_edges_from(removidos[25])
G26 = nx.Graph(G)
G26.remove_edges_from(removidos[26])
G27 = nx.Graph(G)
G27.remove_edges_from(removidos[27])
grafos = [G,G1,G2,G3,G4,G5,G6,G7,G8,G9,G10,G11,G12,G13,G14,G15,G16,G17,G18,G19,
G20,G21,G22,G23,G24,G25,G26,G27]
Agora, vamos salvar uma figura para cada grafo e, usando o comando ffmpeg discutido na postagem passada, fazer um vídeo com a dinâmica.
for time in range(28):
cor = []
for j in range(number_of_nodes):
cor.append(log[time][j]['id'])
cores = []
for j in cor:
if j == 1:
cores.append('red')
else:
cores.append('lightgreen')
#plotando a rede
plt.figure(time, figsize=(12, 8))
plt.axis('off')
pos = nx.fruchterman_reingold_layout(grafos[time])
nx.draw_networkx_nodes(grafos[time],pos,node_size=60,node_color=cores)
nx.draw_networkx_edges(grafos[time],pos,alpha=.4)
plt.title('Infection - Time '+str(time), size=16)
dens = nx.density(grafos[time])
plt.suptitle('Densidade = '+str(dens))
if time < 9:
plt.savefig('/home/neylson/diffusion_model/figuras_escape/image00'+str(time+1)+'.png')
elif time >= 9:
plt.savefig('/home/neylson/diffusion_model/figuras_escape/image0'+str(time+1)+'.png')
plt.show()
Podemos transformar todos os plots em um vídeo para facilitar a visualização com ffmpeg. Aqui está o código para fazer um slide show.
ffmpeg -framerate 1 -i image%03d.png output.mp4
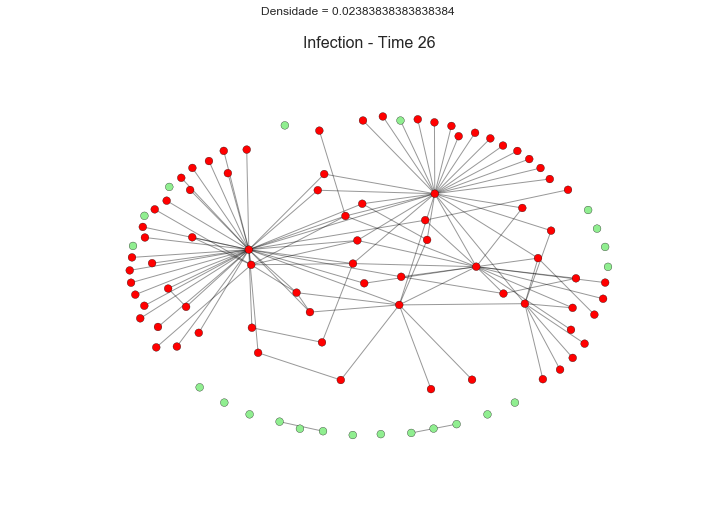
Clique no grafo abaixo para visualizar:
Podemos ver claramente como os agentes que conseguiram “escapar” ficam isolados da rede de zumbis e à salvo. Agora, vamos plotar a dinâmica da densidade da rede. Poderíamos investigar qualquer outra medida comum à análise de redes sociais.
densidades = []
for time in range(28):
dens = nx.density(grafos[time])
densidades.append(dens)
plt.plot(densidades, color='orange')
plt.title('Escape ZombieApokalypse, $P_{inf} = 0.3$, $P_{run} = 0.2$')
plt.xlim(xmax=27)
plt.xlabel('Time')
plt.ylabel('Density')
plt.show()
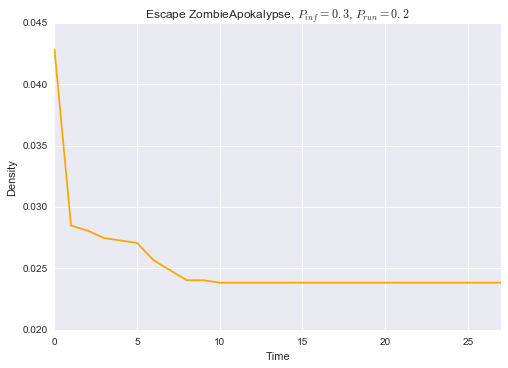
A medida da densidade mostra o quão conectada é a rede. Ela é obtida através do cálculo do número de laços observados sobre o número total de laços possíveis num grafo. Formalmente,
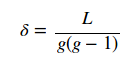
onde g é o número de laços do grafo e L o número de laços observados. O gráfico mostra como a densidade da rede vai abaixando à medida que alguns humanos conseguem escapar e ficar numa posição segura isolados de outros zumbis.
Por hoje é só. Comentários na postagem são sempre bem vindos! Abraços!