Após um encontro marcante com o prof. Davoud Taghawi-Nejad numa disciplina do MQ 2016 de Agent Based Modeling onde fui iniciado à programação em Python, fiquei com “a pulga atrás da orelha” sobre o poder dessa linguagem. Após alguma investigação preliminar, além de descobrir vários comentários de pessoas da área da computação exaltando a praticidade, facilidade e eficiência da linguagem, descobri também uma alta integração com R. Por que isso acontece?
As principais justificativas mobilizadas foram na linha de que há algumas coisas mais fáceis de serem feitas no R e outras mais fáceis de serem feitas no Python. O melhor dos dois mundos estaria na utilização conjunta das duas ferramentas. Agent Based Modeling, por exemplo, seria mais fácil no Python. A elaboração de modelos estatísticos mais complexos, como Modelos Hierárquicos ou os Modelos P* (ERGM’s) para dados relacionais seriam mais fáceis no R.
A partir disso, dedici realizar alguns testes com Python e tentar descobrir este melhor entre os dois mundos. Hoje vamos trabalhar algumas análises básicas de Análises de Redes Sociais (ARS) com o módulo networkx do Python. Tudo foi feito com Python 3.5 usando Spyder. Vamos lá!
import networkx as nx
import pandas as pd
import scipy as sp
from scipy import stats
import matplotlib.pyplot as plt
'''
Importando um arquivo com minha rede pessoal. Você pode tentar com outro arquivo do Pajek (.net) que possuir.
Caso não possua, você pode trabalhar com os dados embutidos no módulo da rede de casamentos das famílias florentinas.
Para isso, use o comando:
G = nx.florentine_families_graph()
'''
G = nx.read_pajek('/home/neylson/Documentos/rede_neylson.net')
G = nx.Graph(G) # Transformando num grafo ao invés de um Multi-grafo
# Plotando a rede
plt.figure(1, figsize=(12, 8)) #definindo o tamanho da figura
pos=nx.fruchterman_reingold_layout(G) #definindo o algoritmo do layout
plt.axis('off') #retira as bordas
nx.draw_networkx_nodes(G,pos,node_size=50) #plota os nodes
nx.draw_networkx_edges(G,pos,alpha=0.4) #plota os ties
plt.title('Egonet - Neylson', size=16) #Título
plt.show() #plota
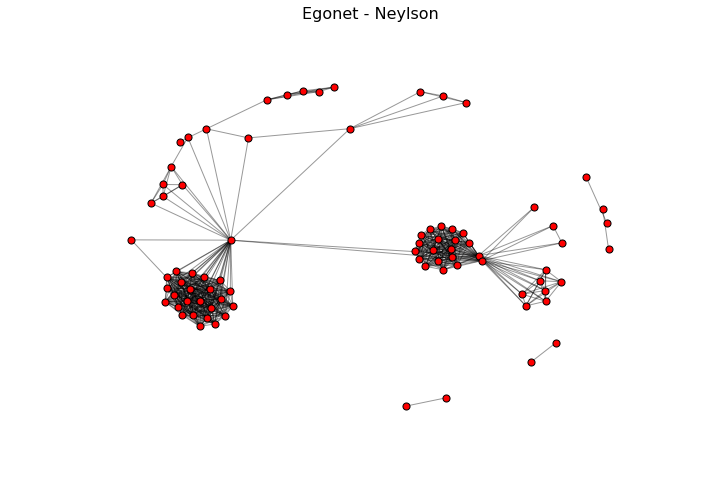
Agora vamos tirar algumas métricas conhecidas da ARS.
# Calculando o grau para cada nó
deg = nx.degree(G)
# Transforma num DataFrame (pandas)
degree = pd.DataFrame.from_dict(data=deg, orient='index')
# Apresenta apenas os valores do dicionário com os graus
deg.values()
dict_values([8, 24, 19, 19, 24, 19, 30, 4, 24, 5, 24, 4, 24, 19, 1, 24, 2, 19, 19, 1, 3, 23, 5, 24, 1, 35, 30, 24, 8, 5, 19, 8, 7, 1, 3, 5, 1, 3, 24, 19, 24, 1, 3, 8, 23, 19, 24, 8, 2, 24, 23, 19, 19, 1, 19, 24, 19, 19, 4, 24, 19, 24, 6, 24, 3, 19, 24, 19, 24, 2, 5, 1, 3, 4, 25, 1, 26, 19, 8, 24, 8, 2])
# Calcula as centralidades de intermediação
bet = nx.betweenness_centrality(G, normalized=False)
# Transforma em DataFrame (pandas)
between = pd.DataFrame.from_dict(data=bet, orient='index')
# Apresenta apenas os valores do dicionário com as centralidades de intermediação
bet.values()
dict_values([0.0, 1.913043478260871, 0.0, 0.0, 1.913043478260871, 0.0, 633.5, 0.0, 1.913043478260871, 0.0, 1.913043478260871, 0.0, 1.913043478260871, 0.0, 0.0, 1.913043478260871, 0.0, 0.0, 0.0, 0.0, 0.0, 1.8695652173913055, 192.0, 1.913043478260871, 0.0, 1461.0434782608695, 633.5, 1.913043478260871, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 4.0, 0.0, 2.0, 1.913043478260871, 0.0, 1.913043478260871, 0.0, 0.0, 0.0, 1.8695652173913055, 0.0, 1.913043478260871, 0.0, 0.0, 1.913043478260871, 0.043478260869565216, 0.0, 0.0, 0.0, 0.0, 1.913043478260871, 0.0, 0.0, 0.0, 1.913043478260871, 0.0, 1.913043478260871, 2.0, 1.913043478260871, 0.0, 0.0, 1.913043478260871, 0.0, 1.913043478260871, 0.0, 0.0, 0.0, 0.0, 0.0, 13.913043478260885, 0.0, 1.913043478260871, 0.0, 0.0, 1.913043478260871, 0.0, 0.0])
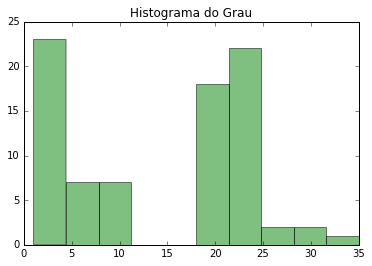
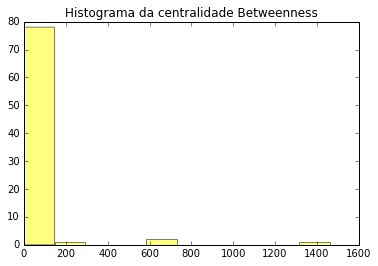
Agora vamos investigar um pouco as distribuições do grau e da centralidade betweeness. Vamos pedir estatísticas descritivas dessas variáveis com o comando stats.describe().
stats.describe(between)
DescribeResult(nobs=82, minmax=(array([ 0.]), array([ 1461.04347826])), mean=array([ 36.3902439]), variance=array([ 35381.05947516]), skewness=array([ 6.192137]), kurtosis=array([ 40.67356702]))
stats.describe(degree)
DescribeResult(nobs=82, minmax=(array([1]), array([35])), mean=array([ 14.12195122]), variance=array([ 96.33062331]), skewness=array([-0.04715037]), kurtosis=array([-1.51965044]))
Vamos agora plotar as distribuições de grau e de centralidade de intermediação em histogramas.
plt.hist(degree, color="green", alpha=.5)
plt.title('Histograma do Grau')
plt.show()
plt.hist(between, color="yellow", alpha=.5)
plt.title('Histograma da centralidade Betweenness')
plt.show()
Vamos investigar a densidade desse grafo. A densidade é uma medida que mostra o quão conectada é uma rede. A densidade delta pode ser definida por

onde g é o número de vértices e L é o número de laços observados. Em suma, esta medida é calculada com o número de laços observados sobre o número de laços possíveis na rede.
# Investigando a densidade
densidade = nx.density(G)
densidade
0.17434507678410116
Agora, vamos plotar a rede novamente fazendo com que o tamanho dos vértices varie por grau e por centralidade de intermediação.
plt.figure(1, figsize=(12, 8))
pos=nx.fruchterman_reingold_layout(G)
plt.axis('off')
nx.draw_networkx_nodes(G,pos,node_size=degree*5)
nx.draw_networkx_edges(G,pos,alpha=0.4)
plt.title('Egonet - Neylson\nTamanho = Degree', size=16)
plt.show()
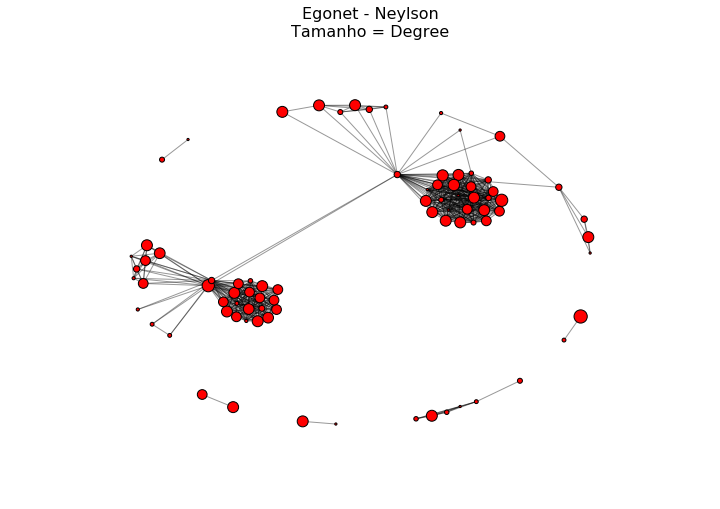
Agora o tamanho variando por centralidade “betweenness”.
plt.figure(1, figsize=(12, 8))
pos=nx.fruchterman_reingold_layout(G)
plt.axis('off')
nx.draw_networkx_nodes(G,pos,node_size=between)
nx.draw_networkx_edges(G,pos,alpha=0.4)
plt.title('Egonet - Neylson\nTamanho = Centralidade Betweenness', size=16)
plt.show()

É muito comum em redes extraírmos apenas o componente gigante ou componente principal, isto é, a maior estrutura conectada da rede. Algumas medidas só são possíveis numa estrutura conectada. Um exemplo é a medida de diâmetro, ou seja, a maior distância geodésica encontrada na rede. É necessário extrair o componente principal porque se tentarmos calcular o diâmetro de uma estrutura disconexa nos depararemos com uma distância infinita. Veja como a densidade muda dentro do componente principal.
# Extraindo o componente gigante
giant = max(nx.connected_component_subgraphs(G), key=len)
#Calculando a densidade
dens = nx.density(giant)
dens
0.247585601404741
nx.diameter(giant)
4
Vamos agora plotar o componente principal.
plt.figure(1, figsize=(12,8))
pos=nx.fruchterman_reingold_layout(giant)
plt.axis('off')
nx.draw_networkx_nodes(giant,pos,node_size=60,node_color='lightgreen')
nx.draw_networkx_edges(giant,pos,alpha=.4)
plt.title('Egonet - Neylson\nGiant Component', size=16)
plt.show()

Vamos agora investigar o grau médio do componente principal.
grau = pd.DataFrame.from_dict(nx.degree(giant), orient='index')
print('Grau médio do componente principal: ' + str(sp.mean(grau)[0]))
Grau médio do componente principal: 16.5882352941
Vamos investigar as estatísticas descritivas da variável grau para o componente principal.
stats.describe(grau)
DescribeResult(nobs=68, minmax=(array([2]), array([35])), mean=array([ 16.58823529]), variance=array([ 79.79806848]), skewness=array([-0.39919466]), kurtosis=array([-1.16243315]))
Agora, vamos investigar a assortatividade do componente principal. A assortatividade é uma medida de correlação que mostra se nós com grau alto se conectam a nós de mesmo grau ou parecidos (assortativa) ou se nós de grau alto se conectam com nós de graus diferentes (disassortativo). A medida é calculada por
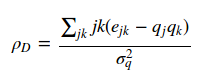
onde ejk é o excesso conjunto da probabilidade dos graus de j e de k, q é a distribuição normalizada do grau excedente de um nó aleatório e o denominador sigma q ao quadrado é a variância de q. Vamos ao escore:
r = nx.degree_assortativity_coefficient(giant)
r
0.35015909173160908
O rho de 0.35 mostra que a rede é assortativa, ou seja, nós com alto grau relacionam-se entre si.
Por hoje é isso! Dúvidas, comentários, elogios e críticas, deixe aqui no final do post. Grande abraço!