Olá. Os bancos de dados que vamos usar nesta parte da aula estão disponíveis em http://bit.ly/2dnrHmZ.
Importando bancos de dados
Podemos importar um banco de dados no R usando os comandos read.table().
options(scipen=999)
dados <- read.table("enade_2014_amostra.csv", sep = ";", stringsAsFactors = F, header = T)
Há outros comandos para importar bancos de dados em estruturas específicas, como separados por vírgulas (.csv), separados por ponto-e-vírgula, separados por tab (.tsv), bancos de dados em formato fixo (como a PNAD). Você pode investigar cada um deles usando o comando help() ou sua versão compacta, ?.
help("read.csv")
?read.fwf
?read.csv2
Importando dados com o pacote readr
Um dos maiores desenvolvedores para linguagem R, Hadley Wickham, desenvolveu um pacote muito eficiente para leitura de bancos de dados chamado readr. Como sabemos que trata-se de um arquivo .csv separado por ponto-e-vírgula, devemos usar o comando read_csv2. Vamos experimentá-lo comparando seu desempenho com o comando da base do R:
system.time(dados <- read.csv2("enade_2014_amostra.csv", stringsAsFactors = F, header = T))
## user system elapsed
## 0.548 0.000 0.544
library(readr)
system.time(dados <- read_csv2("enade_2014_amostra.csv", col_names = T))
## user system elapsed
## 0.128 0.000 0.128
Veja como a função read_csv2() é mais de 3 vezes mais rápida do que a função base!!! O Wickham tem ainda vários outros pacotes desenvolvidos para manipulação de dados string, manipulação de bancos de dados, transformação de variáveis, dentre outros. Esses pacotes podem tornar a nossa vida bem mais fácil! Veja uma apresentação sobre o hadleyverse, universo de Hadley em http://barryrowlingson.github.io/hadleyverse.
Para importar dados de outros programas como SPSS, Stata ou SAS, você pode usar o pacote foreign.
library(foreign)
?read.spss # lê SPSS
?read.dta # lê Stata
?read.ssd # lê SAS
?read.xport # lê SAS
Bônus: Introdução ao ggplot2
ggplot2 é um pacote desenvolvido por (adivinha?) Hadley Wickham para a construção de gráficos de alta qualidade e alta customização. Gráficos desse pacote se tornaram um standard no meio acadêmico podendo ser encontrados nas principais revistas de análise quantitativa.
Sua sintaxe é a seguinte:
ggplot(data = "banco de dados", aes(x = "vetor x", y = "vetor y")) + tipo de gráfico (podem ser vários aninhados)
Vamos repetir alguns gráficos gerados com o banco de dados iris agora com o pacote ggplot2.
library(ggplot2)
data(iris)
# Gerando um histograma
ggplot(data=iris, aes(x=Petal.Length))+geom_histogram()

# Gerando um scatterplot
ggplot(data=iris, aes(x=Petal.Length, y=Sepal.Length))+geom_point()

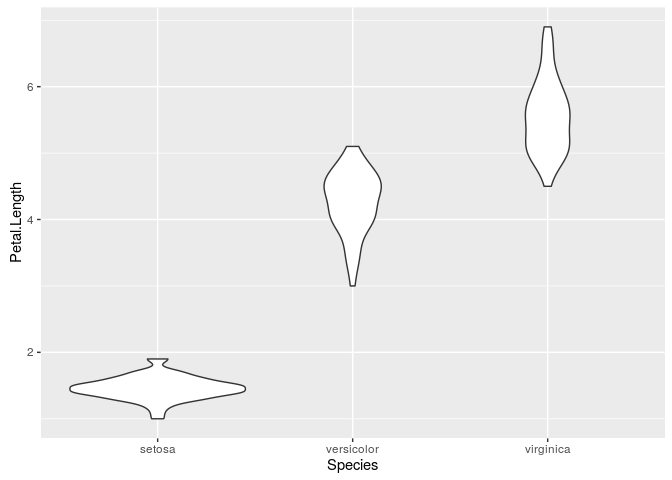
# Gerando um boxplot e um violinplot
ggplot(data=iris, aes(x=Species, y=Petal.Length))+geom_boxplot()

ggplot(data=iris, aes(x=Species, y=Petal.Length))+geom_violin()
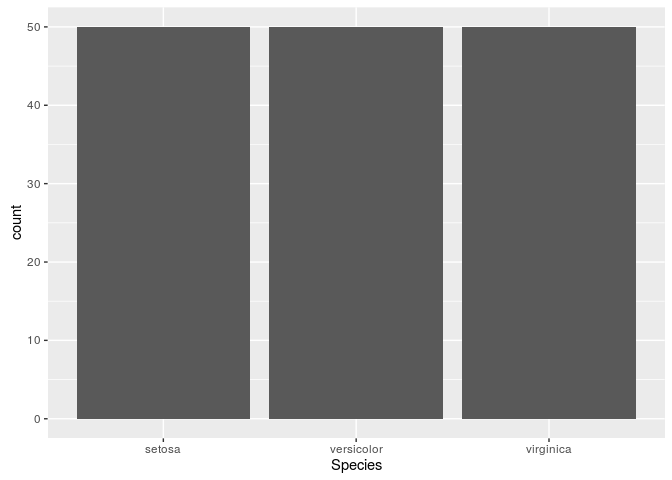
# Gerando um gráfico de barras
ggplot(data=iris, aes(x=Species))+geom_bar()
# Podemos inclusive plotar uma reta de regressão
ggplot(data=iris, aes(x=Petal.Length, y=Sepal.Length))+geom_point()+geom_smooth(method="lm")

Algumas análises com dados da PNAD
Vamos realizar algumas análises com os dados da PNAD 2012. Primeiro importamos o banco de dados.
library(foreign)
pnad <- read.spss("pes_2012.sav", to.data.frame = T)
head(pnad)
## V0101 UF V0302 V8005 V0404 V4803 V4718 V4720 V4729
## 1 2012 Rondônia Masculino 48 Branca 15 anos ou mais 3000 3000 232
## 2 2012 Rondônia Feminino 48 Branca 15 anos ou mais 3000 3000 232
## 3 2012 Rondônia Feminino 23 Branca 15 anos ou mais 1100 1100 232
## 4 2012 Rondônia Feminino 21 Branca 14 anos 1100 1100 232
## 5 2012 Rondônia Feminino 54 Branca 15 anos ou mais NA 460 232
## 6 2012 Rondônia Masculino 56 Preta 15 anos ou mais 10000 10000 232
Vamos ver a variável sexo (V0302):
library(descr)
freq(pnad$V0302)

## pnad$V0302
## Frequência Percentual
## Masculino 176397 48.67
## Feminino 186054 51.33
## Total 362451 100.00
Vamos verificar a idade (V8005) média, e depois a idade média de homens e mulheres. Podemos verificar a idade por grupos de sexo fazendo subsetting ou realizando um teste de médias.
mean(pnad$V8005)
## [1] 32.63801
# Média ponderada pelo peso amostral
weighted.mean(pnad$V8005, pnad$V4729)
## [1] 33.0607
# Média por grupos de sexo
mean(pnad$V8005[pnad$V0302 == "Masculino"])
## [1] 31.62186
mean(pnad$V8005[pnad$V0302 == "Feminino"])
## [1] 33.60142
t.test(pnad$V8005~pnad$V0302)
##
## Welch Two Sample t-test
##
## data: pnad$V8005 by pnad$V0302
## t = -28.734, df = 362230, p-value < 0.00000000000000022
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -2.114581 -1.844524
## sample estimates:
## mean in group Masculino mean in group Feminino
## 31.62186 33.60142
Vamos verificar agora a variável cor (V0404). Vamos elaborar uma tabela de contingência cor X sexo.
freq(pnad$V0404)
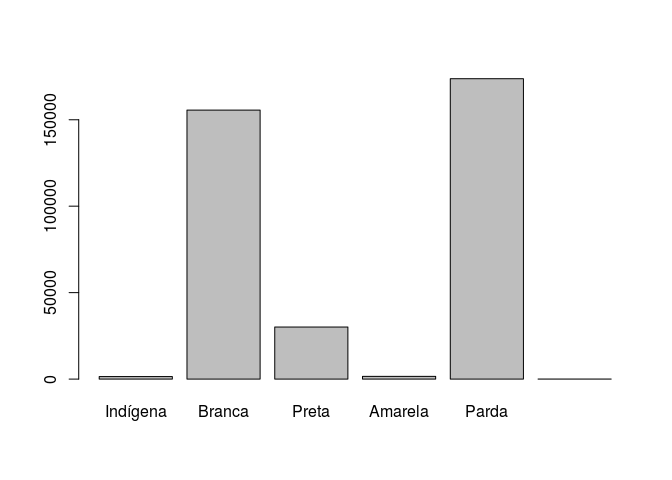
## pnad$V0404
## Frequência Percentual
## Indígena 1435 0.395916
## Branca 155595 42.928561
## Preta 30120 8.310089
## Amarela 1550 0.427644
## Parda 173733 47.932824
## Sem declaração 18 0.004966
## Total 362451 100.000000
table(pnad$V0404,pnad$V0302)
##
## Masculino Feminino
## Indígena 721 714
## Branca 73465 82130
## Preta 15222 14898
## Amarela 682 868
## Parda 86298 87435
## Sem declaração 9 9
Agora vamos investigar a variável renda mensal do trabalho principal. Para isso, é preciso codificar o valor 999999999999 como NA.
summary(pnad$V4718)
## Min. 1st Qu. Median Mean 3rd Qu.
## 0 622 800 26260000000 1500
## Max. NA's
## 1000000000000 188912
# Veja que, após a recodificação dos NA's, as medidas estatísticas mudam
pnad$V4718[pnad$V4718 >= 999999999999] = NA
summary(pnad$V4718)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0 622 800 1343 1400 350000 193470
hist(pnad$V4718)
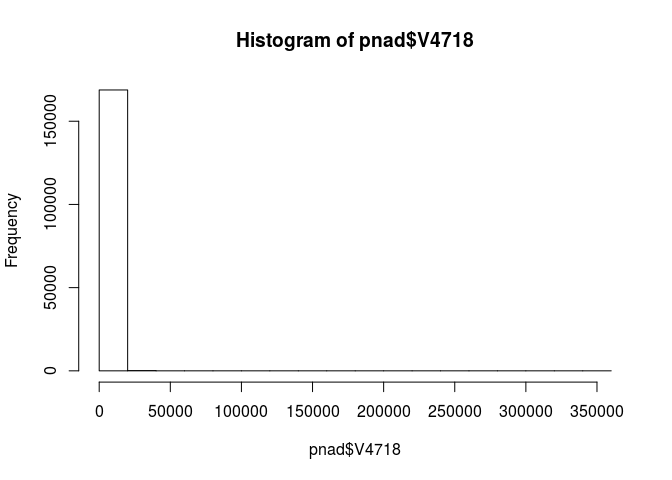
Vamos testar algumas diferenças de salários por sexo e cor. Para testar por cor, vamos criar uma variável dummy branco. Para isso, usaremos o comando ifelse(). Ele funciona da seguinte maneira: se a condição determinada for cumprida, atribui-se o primeiro valor. Se não, atribui-se o segundo valor.
# Testando por sexo
t.test(pnad$V4718~pnad$V0302)
##
## Welch Two Sample t-test
##
## data: pnad$V4718 by pnad$V0302
## t = 36.656, df = 163240, p-value < 0.00000000000000022
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 421.982 469.657
## sample estimates:
## mean in group Masculino mean in group Feminino
## 1532.572 1086.752
# Criando a dummy branco
# Se pnad$V0404 for igual a "branca", atribua 1. Se não, atribua 0.
pnad$branco <- ifelse(pnad$V0404 == "Branca", 1, 0)
pnad$branco <- as.factor(pnad$branco) # transforma em factor
levels(pnad$branco) <- c("Não Branco","Branco") # coloca os labels
freq(pnad$branco, plot=F) # verifica a distribuição
## pnad$branco
## Frequência Percentual
## Não Branco 206856 57.07
## Branco 155595 42.93
## Total 362451 100.00
# Será que brancos ganham mais, menos, ou igual a não brancos no Brasil?
t.test(pnad$V4718~pnad$branco)
##
## Welch Two Sample t-test
##
## data: pnad$V4718 by pnad$branco
## t = -51.066, df = 92293, p-value < 0.00000000000000022
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -750.1254 -694.6719
## sample estimates:
## mean in group Não Branco mean in group Branco
## 1027.188 1749.587
Vamos testar agora algumas correlações entre renda, escolaridade e idade. Para isso, é necessário retirar os NA’s.
pnad_semna <- na.omit(pnad) # tira NA's e guarda no objeto pnad_semna
# Renda, escolaridade e idade
cor(cbind(pnad_semna$V4718, as.numeric(pnad_semna$V4803), pnad_semna$V8005))
## [,1] [,2] [,3]
## [1,] 1.0000000 0.2605251 0.1046775
## [2,] 0.2605251 1.0000000 -0.2547903
## [3,] 0.1046775 -0.2547903 1.0000000
Regressão linear - Exemplo com ENADE 2014
Vamos montar um modelinho de regressão para tentar explicar o desempenho dos alunos no ENADE como função do sexo, da idade e da cor. Para isso, primeiro devemos verificar a distribuição da variável resposta.
enade <- read_csv2("enade_2014_amostra.csv", col_names = T)
hist(enade$nt_ger, col = "blue")
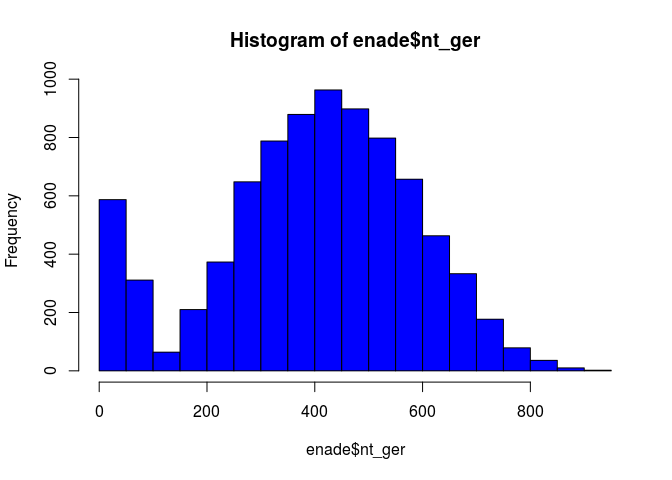
A variável possui distribuição normal e portanto é uma boa variável para aplicar regressão linear por MQO. Agora, após, ver algumas estatísticas descritivas, vamos montar o modelo:
summary(enade$nt_ger)
## Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
## 0.0 292.0 414.0 399.6 528.0 943.0 1724
# Colocando NA's nas não respostas da variável sexo
enade$tp_sexo[enade$tp_sexo == "N"] = NA
freq(enade$tp_sexo, plot=F)
## enade$tp_sexo
## Frequência Percentual % Válido
## F 5744 57.44 57.45
## M 4254 42.54 42.55
## NA's 2 0.02
## Total 10000 100.00 100.00
# Idade
summary(enade$nu_idade)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 18.00 23.00 27.00 29.89 34.00 73.00
# Cor
class(enade$qe_i2)
## [1] "character"
enade$qe_i2 <- as.factor(enade$qe_i2) # transformando em factor
# colocando os labels
levels(enade$qe_i2) <- c("Branco","Negro","Pardo","Amarelo","Indígena")
freq(enade$qe_i2, plot=F)
## enade$qe_i2
## Frequência Percentual % Válido
## Branco 4606 46.06 52.9791
## Negro 893 8.93 10.2715
## Pardo 2988 29.88 34.3685
## Amarelo 129 1.29 1.4838
## Indígena 78 0.78 0.8972
## NA's 1306 13.06
## Total 10000 100.00 100.0000
A sintaxe do modelo de regressão funciona da seguinte forma:
lm(dependente ~ preditor1 + preditor2 + preditor3, data = banco de dados)
# Montando o modelo
modelo <- lm(nt_ger ~ tp_sexo + nu_idade + qe_i2, data=enade)
summary(modelo) # apresenta os resultados do modelo
##
## Call:
## lm(formula = nt_ger ~ tp_sexo + nu_idade + qe_i2, data = enade)
##
## Residuals:
## Min 1Q Median 3Q Max
## -425.92 -106.49 13.69 127.53 521.92
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 448.8788 7.8895 56.896 < 0.0000000000000002 ***
## tp_sexoM 0.6301 4.1269 0.153 0.878656
## nu_idade -1.2085 0.2409 -5.017 0.000000535724 ***
## qe_i2Negro -25.9165 6.9206 -3.745 0.000182 ***
## qe_i2Pardo -28.6309 4.4442 -6.442 0.000000000124 ***
## qe_i2Amarelo -19.1198 16.4444 -1.163 0.244987
## qe_i2Indígena -50.1873 21.4993 -2.334 0.019600 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 183.4 on 8235 degrees of freedom
## (1758 observations deleted due to missingness)
## Multiple R-squared: 0.009782, Adjusted R-squared: 0.009061
## F-statistic: 13.56 on 6 and 8235 DF, p-value: 0.000000000000002249
Podemos interpretar este modelo da seguinte forma:
Homens não tem diferença estatisticamente significante das mulheres em relação à nota geral. Para cada 1 ano a mais de idade, a nota geral diminui, em média, 1.21 pontos. No caso da variável Cor, por se tratar de uma variável categórica, todos os coeficientes serão interpretados em relação à categoria de referência, a que foi retirada. Neste caso, negros tem, em média, uma nota 25.9 pontos menor que brancos; pardos tem, em média, uma nota 28.6 pontos menor que brancos, e indígenas tem, em média, uma nota -50 pontos menor que brancos mantendo-se todas as demais variáveis constantes. O coeficiente para a categoria amarelo não foi estatisticamente significativo, ou seja, a diferença entre as notas desse grupo e dos brancos é estatisticamente igual a 0.
Agora vamos avaliar nosso modelo. O R nos dá alguns gráficos default de avaliação.
# gráficos de avaliação
plot(modelo)
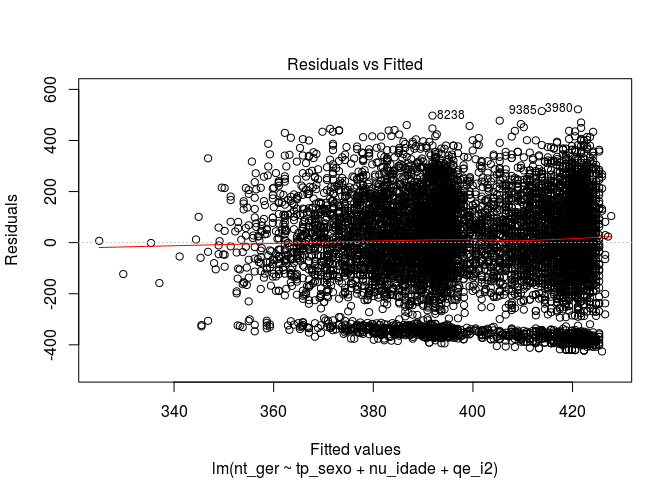
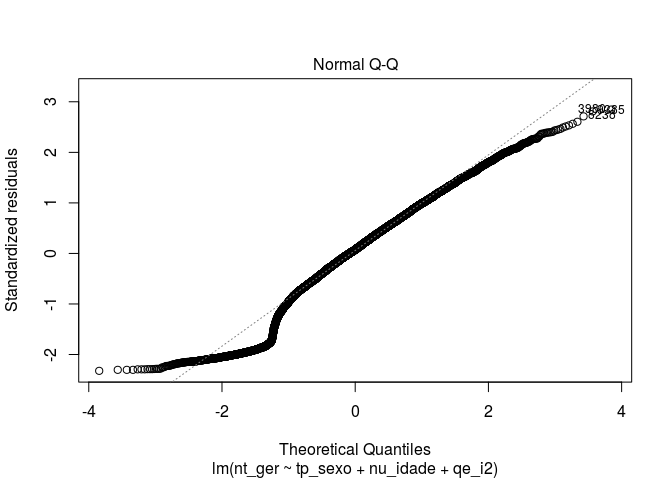
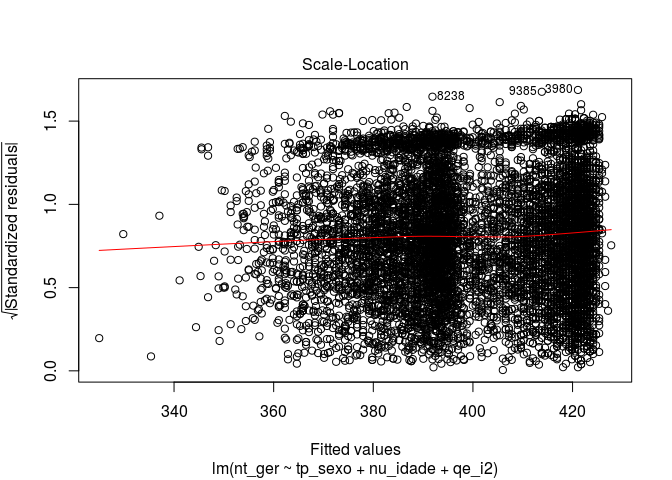
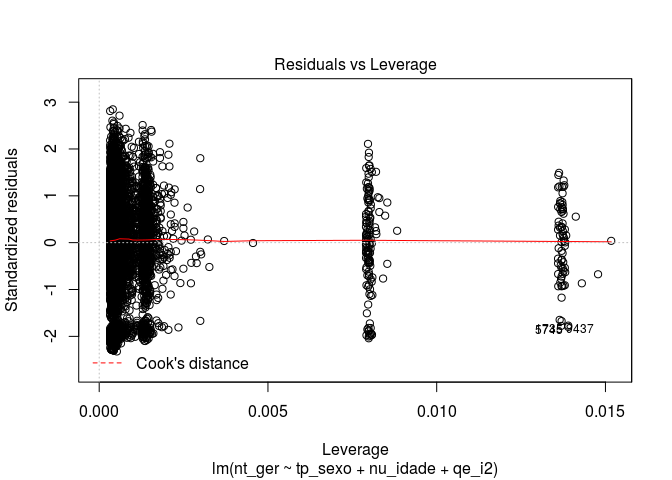
Para realizar uma análise dos resíduos da regressão, podemos tirar um histograma. O comando residuals() extrai os resíduos de um modelo estatístico.
# Histograma dos resíduos
hist(residuals(modelo), col = "red")

Depois disso, podemos plotar a reta de regressão usando o comando plot() e o comando abline(). O comando abline() toma como argumentos o intercepto e a inclinação (coeficiente) da variável que desejamos plotar.
# Plotando a reta de regressão
coef(modelo) # verificando apenas os coeficientes do modelo
## (Intercept) tp_sexoM nu_idade qe_i2Negro qe_i2Pardo
## 448.8788071 0.6300838 -1.2084605 -25.9164527 -28.6308728
## qe_i2Amarelo qe_i2Indígena
## -19.1197937 -50.1872827
plot(enade$nu_idade, enade$nt_ger, pch=19) # plotando as variáveis
abline(a=448.8764, b=-1.2085, col="red", lwd = 2) #plotando uma reta com intercepto e slope
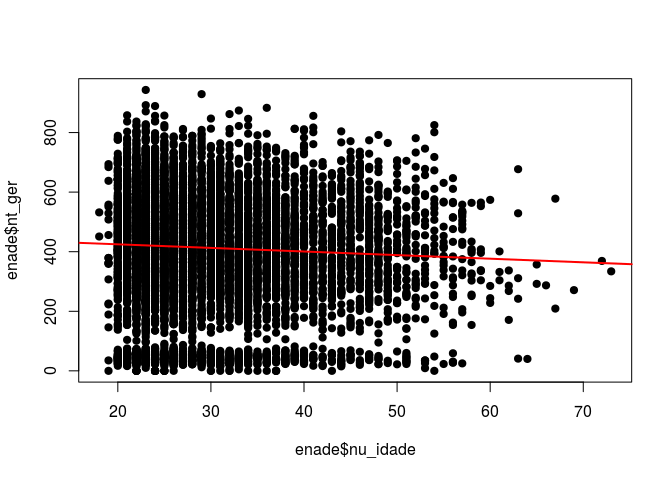
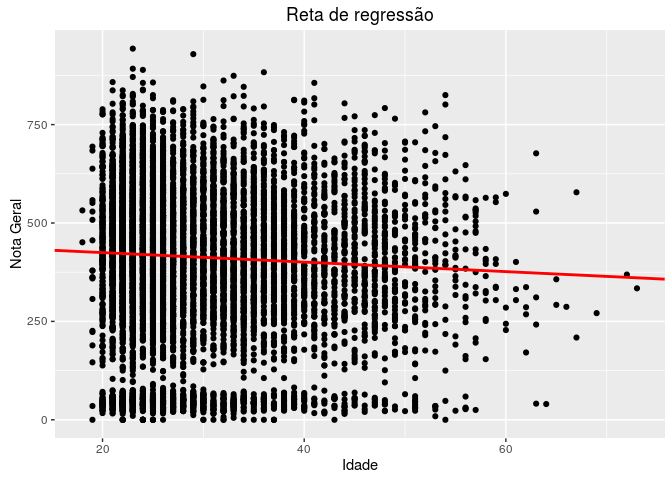
# BONUS: o mesmo gráfico com ggplot2
library(ggplot2)
ggplot(enade, aes(nu_idade, nt_ger))+geom_point()+
geom_abline(intercept = 448.8764, slope = -1.2085, col="red", lwd=1)+
labs(title="Reta de regressão", x="Idade", y="Nota Geral")