Análises preliminares
Vamos analisar um banco de dados imbutido no R com dados de medidas de tamanho e espessura de pétalas e sépalas de 3 diferentes espécies de flores.
options(scipen=999) # Tira a notação científica do tipo 2e-16
data(iris)
names(iris) # Retorna o nome das variáveis
## [1] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width"
## [5] "Species"
dim(iris) # Dimensões do banco de dados
## [1] 150 5
head(iris) # Mostra as primeiras colunas
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 5.1 3.5 1.4 0.2 setosa
## 2 4.9 3.0 1.4 0.2 setosa
## 3 4.7 3.2 1.3 0.2 setosa
## 4 4.6 3.1 1.5 0.2 setosa
## 5 5.0 3.6 1.4 0.2 setosa
## 6 5.4 3.9 1.7 0.4 setosa
tail(iris) # Mostra as últimas colunas
## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 145 6.7 3.3 5.7 2.5 virginica
## 146 6.7 3.0 5.2 2.3 virginica
## 147 6.3 2.5 5.0 1.9 virginica
## 148 6.5 3.0 5.2 2.0 virginica
## 149 6.2 3.4 5.4 2.3 virginica
## 150 5.9 3.0 5.1 1.8 virginica
View(iris) # Visualizar o banco de dados completo
Vamos olhar primeiro para a classe de cada variável:
class(iris[[1]])
## [1] "numeric"
class(iris[[2]])
## [1] "numeric"
class(iris[[3]])
## [1] "numeric"
class(iris[[4]])
## [1] "numeric"
class(iris[[5]])
## [1] "factor"
As quatro primeiras variáveis são numéricas. A última é do tipo factor, uma classe que ainda não abordamos. Faremos isso mais adiante. Vamos nos concentrar agora em possibilidades de análises para dados do tipo numeric.
Podemos pedir um conjunto de estatísticas descritivas dos dados com o comando summary()
summary(iris)
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100
## 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300
## Median :5.800 Median :3.000 Median :4.350 Median :1.300
## Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
## 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
## Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
## Species
## setosa :50
## versicolor:50
## virginica :50
##
##
##
Podemos usar o mesmo comando para tirar estatísticas descritivas de cada variável
summary(iris$Sepal.Length)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 4.300 5.100 5.800 5.843 6.400 7.900
ou pedir as estatísticas que nos interessam. Por exemplo:
mean(iris$Sepal.Length) # Média
## [1] 5.843333
median(iris$Sepal.Length) # Mediana
## [1] 5.8
var(iris$Sepal.Length) # Variância
## [1] 0.6856935
sd(iris$Sepal.Length) # Desvio Padrão
## [1] 0.8280661
max(iris$Sepal.Length) # Máximo
## [1] 7.9
min(iris$Sepal.Length) # Mínimo
## [1] 4.3
quantile(iris$Sepal.Length) # Quartis
## 0% 25% 50% 75% 100%
## 4.3 5.1 5.8 6.4 7.9
quantile(iris$Sepal.Length, probs =c(0,.1,.2,.3,.4,.5,.6,.7,.8,.9,1)) # Decis
## 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%
## 4.30 4.80 5.00 5.27 5.60 5.80 6.10 6.30 6.52 6.90 7.90
Algumas estatísticas comuns
Vamos investigar algumas relações entre essas variáveis. Primeiro, vamos tirar uma matriz de correlações.
cor(iris[,1:4]) # Correlaciona as variáveis de 1 a 4
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Sepal.Length 1.0000000 -0.1175698 0.8717538 0.8179411
## Sepal.Width -0.1175698 1.0000000 -0.4284401 -0.3661259
## Petal.Length 0.8717538 -0.4284401 1.0000000 0.9628654
## Petal.Width 0.8179411 -0.3661259 0.9628654 1.0000000
cor(iris$Sepal.Length, iris$Petal.Length) # Correlação entre duas variáveis
## [1] 0.8717538
cor.test(iris$Sepal.Length, iris$Petal.Length) # Correlação com teste estatístico
##
## Pearson's product-moment correlation
##
## data: iris$Sepal.Length and iris$Petal.Length
## t = 21.646, df = 148, p-value < 0.00000000000000022
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.8270363 0.9055080
## sample estimates:
## cor
## 0.8717538
plot(iris$Sepal.Length, iris$Petal.Length) # produz um scatterplot
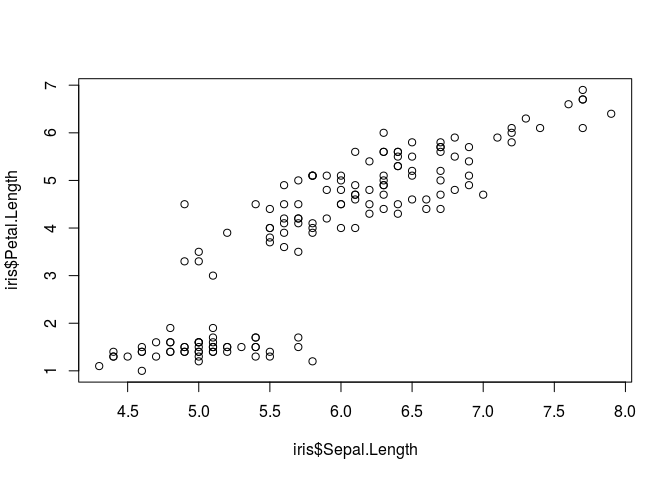
Podemos fazer algumas seleções (subsettings) em nossos dados caso queiramos investigar um grupo específico. Neste caso, vamos olhar para algumas estatísticas das flores pertencentes apenas ao grupo virginica.
# Seleciono as linhas em que a variável Species é igual ao character "virginica"
summary(iris[iris$Species == "virginica", ])
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Min. :4.900 Min. :2.200 Min. :4.500 Min. :1.400
## 1st Qu.:6.225 1st Qu.:2.800 1st Qu.:5.100 1st Qu.:1.800
## Median :6.500 Median :3.000 Median :5.550 Median :2.000
## Mean :6.588 Mean :2.974 Mean :5.552 Mean :2.026
## 3rd Qu.:6.900 3rd Qu.:3.175 3rd Qu.:5.875 3rd Qu.:2.300
## Max. :7.900 Max. :3.800 Max. :6.900 Max. :2.500
## Species
## setosa : 0
## versicolor: 0
## virginica :50
##
##
##
# Seleciono apenas os casos da variável Petal.Length que pertençam ao grupo "virginica"
mean(iris$Petal.Length[iris$Species == "virginica"])
## [1] 5.552
var(iris$Petal.Length[iris$Species == "virginica"])
## [1] 0.3045878
sd(iris$Petal.Length[iris$Species == "virginica"])
## [1] 0.5518947
Atenção!
-
Veja que no caso de summary, usamos vírgula porque especificamos no subsetting linhas e colunas. Quando usamos os comandos
mean(),var()esd(), não usamos vírgula pois trata-se de vetores numéricos, ou seja, especificamos apenas posições. -
Para estabelecer uma relação de igualdade no R usamos
==(igual, igual) pois=(igual) é um símbolo de atribuição (lembram?). Outros comparativos são>(maior que),<(menor que),<=, (menor ou igual),>=(maior ou igual),!=(diferente).
Podemos fazer um teste de duas médias, ou teste T de Student. Testaremos se dois grupos tem médias estatisticamente diferentes ou não. Para isso, primeiro, vamos criar um novo objeto apenas com os dados de duas espécies. Veja bem que esse tipo de teste é feito quando se tem uma variável numérica e uma variável categórica com duas categorias.
# Selecionando as linhas em que Species seja DIFERENTE de "setosa".
dados <- iris[iris$Species != "setosa",]
t.test(dados$Petal.Length~dados$Species)
##
## Welch Two Sample t-test
##
## data: dados$Petal.Length by dados$Species
## t = -12.604, df = 95.57, p-value < 0.00000000000000022
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -1.49549 -1.08851
## sample estimates:
## mean in group versicolor mean in group virginica
## 4.260 5.552
boxplot(dados$Petal.Length~dados$Species)
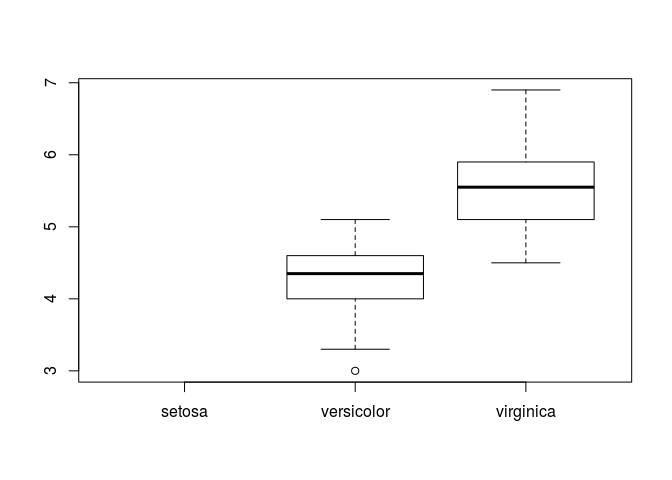
Neste caso, os grupos tem médias estatisticamente diferentes.
Para testar se médias de mais de dois grupos são estatisticamente diferentes, use a análise de variância, ou ANOVA. Vamos testar se existe diferença estatística entre uma das médias da variável Petal.Length para os três grupos de espécies.
summary(aov(iris$Petal.Length~iris$Species))
## Df Sum Sq Mean Sq F value Pr(>F)
## iris$Species 2 437.1 218.55 1180 <0.0000000000000002 ***
## Residuals 147 27.2 0.19
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Neste caso, pelo menos 1 dos grupos tem média estatisticamente diferente dos demais.
Variáveis FACTOR
As variáveis de classe factor são variáveis categóricas. Nessa classe, cada categoria tem um label. Podemos criar uma variável categórica entrando com os dados e definindo os labels, por exemplo:
sexo <- factor(x = c("Feminino","Masculino","Feminino","Masculino","Feminino","Feminino"),
levels = c("Feminino","Masculino"))
sexo
## [1] Feminino Masculino Feminino Masculino Feminino Feminino
## Levels: Feminino Masculino
Há uma função excelente implementada no pacote descr para tabela de frequências de uma variável categórica. Trata-se da função freq(). Para usá-la, primeiro, se ele não estiver instalado, podemos instalá-lo com o comando install.packages(). Segundo, precisamos carregar o pacote no ambiente.
install.packages("descr", dependencies = T) # Instala também as dependências do pacote.
library(descr)
freq(sexo)
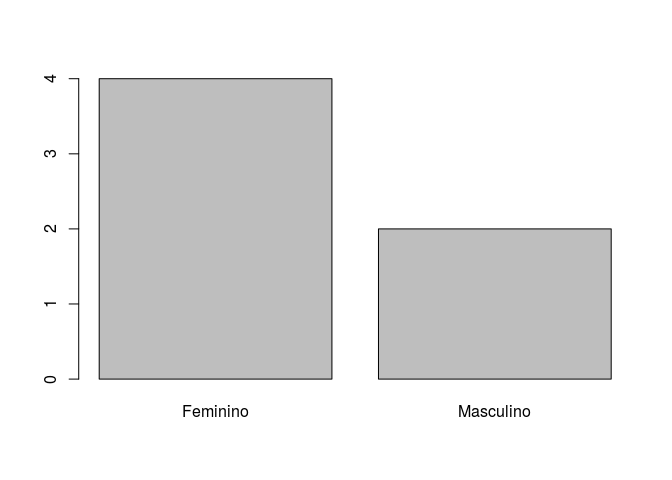
## sexo
## Frequência Percentual
## Feminino 4 66.67
## Masculino 2 33.33
## Total 6 100.00
Vamos usar essa mesma função para analisar a variável Species do banco iris.
freq(iris$Species)
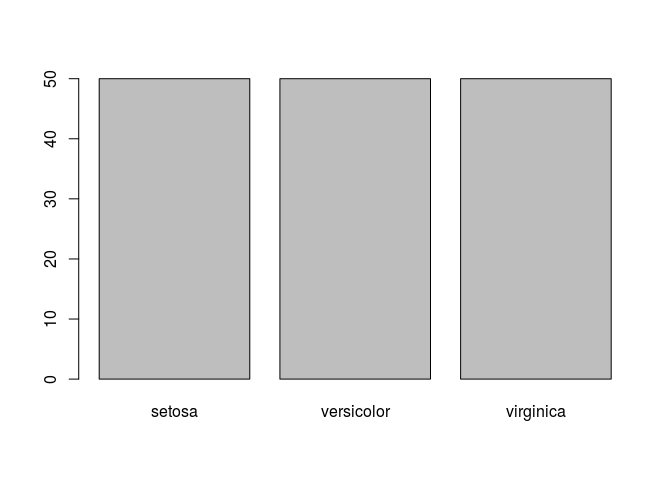
## iris$Species
## Frequência Percentual
## setosa 50 33.33
## versicolor 50 33.33
## virginica 50 33.33
## Total 150 100.00
Guarde esse comando. Ele é bastante útil.
Gráficos
Visualização de dados não é algo trivial e há vários estudos interessantes sobre o assunto. Apresentarei aqui apenas algumas dicas básicas.
Para visualizar a distribuição de uma variável, usamos um histograma.
hist(iris$Petal.Length)
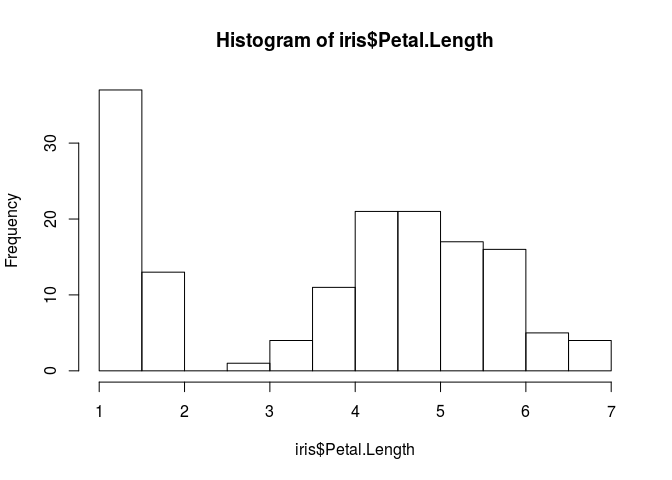
Podemos adicionar um label para o eixo x, para o eixo y, um título mais bonito e uma cor no gráfico para que ele fique um pouco mais simpático:
hist(iris$Petal.Length, xlab = "Comprimento da Pétala", ylab="Frequência" ,main="Histograma do Comprimento da Pétala", col="green")
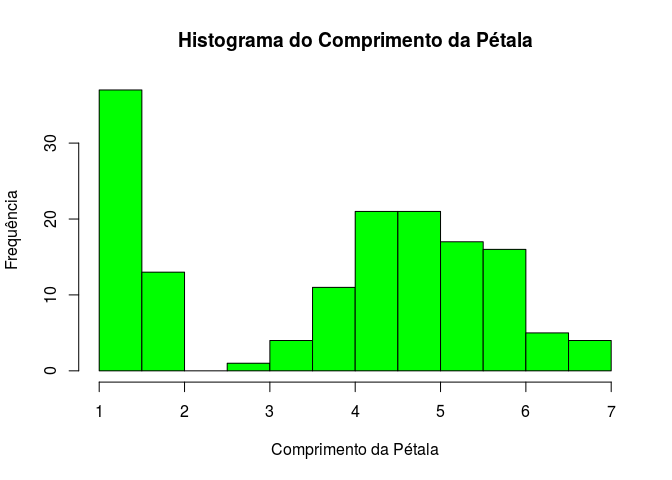
Para visualizar duas variáveis numéricas, podemos usar um scatterplot como fizemos acima.
plot(iris$Petal.Length, iris$Sepal.Length)
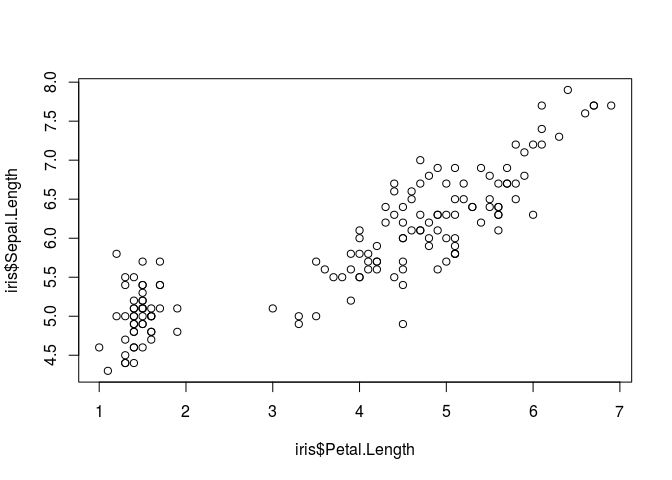
Para visualizar diferenças de variáveis numéricas entre grupos, podemos usar boxplots.
boxplot(iris$Petal.Length~iris$Species)
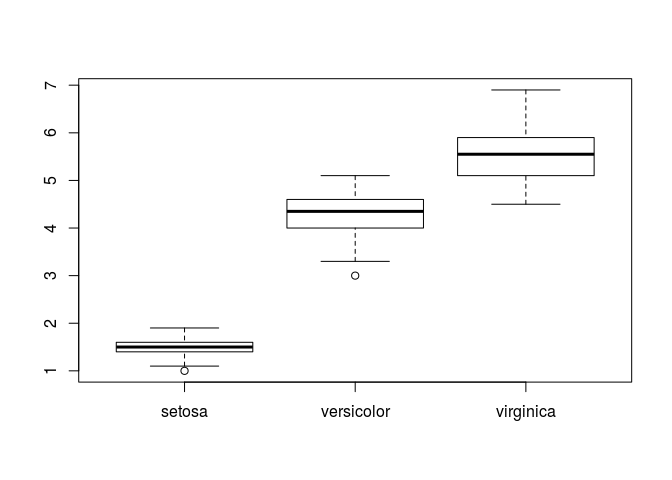
Podemos ainda plotar as frequências de uma variável categórica:
barplot(table(iris$Species))
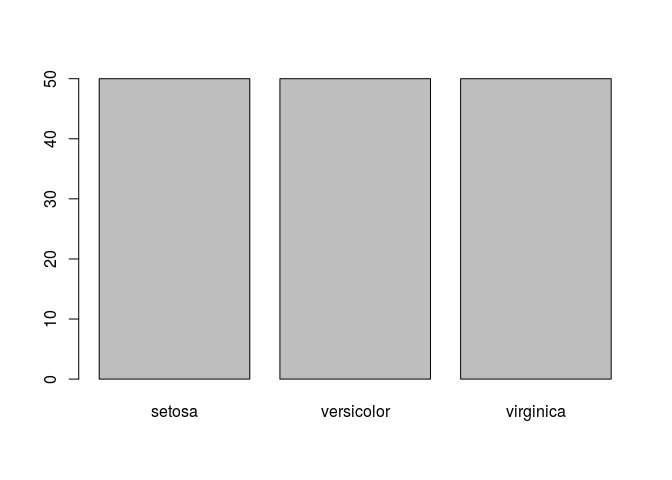
Veja que o comando freq() que utilizamos mais cedo já produz esse gráfico por default.